上次准备解读人口普查数据中的出生人口数据时,上网随便搜搜能搜到大把大把内容。而这次准备解读死亡人口数据之前,也依照惯例先上网搜搜已有的内容1,从数量上对比的话,显然是远远少于出生人口相关内容的2。和出生相比,单纯论及死亡的话,人类的死亡并不会给世界或者人类的发展造成什么问题。
本文探索的方向仅仅在于人口死亡率或死亡人口数在不同情况下的差异和变化,不涉及原因分析或结果预测。本次整理的数据来源有三,《中国人口普查年鉴2020》、《中国2010年人口普查资料》、《中国2000年人口普查资料》,整理好的数据分别是这三个年份在全国各地区分性别与月份、性别与年龄、性别与受教育程度、性别与婚姻状况等维度的死亡人口、人口数据。
1. 导入数据 🔗
library(ggplot2)
library(data.table)
library(readxl)
# 2 各地区分年龄、性别的死亡人口
data2 <- read_xlsx('data/我国人口普查数据-死亡人口数据整理.xlsx', sheet = 2)
# 5 全国分年龄、性别的死亡人口状况
data5 <- read_xlsx('data/我国人口普查数据-死亡人口数据整理.xlsx', sheet = 5)
# 6 各地区分性别、年龄的人口
data6 <- read_xlsx('data/我国人口普查数据-死亡人口数据整理.xlsx', sheet = 6)
2. 数据处理 🔗
点击查看数据处理的 R 代码
# 查看缺失值 sapply(data2, function(x) sum(is.na(x))) sapply(data5, function(x) sum(is.na(x))) sapply(data6, function(x) sum(is.na(x))) # 缺失值全都填0 for (i in 1:ncol(data2)) {data2[, i][is.na(data2[, i])] <- 0} ############################## ##将data2和data6合并计算死亡率 # 2 各地区分年龄、性别的死亡人口 data2 <- as.data.table(data2) data2 <- melt( data2[, -c('死亡人口-合计', '死亡人口-男', '死亡人口-女')], id.vars = c('year', 'type', 'area'), measure.vars = patterns('计$', '男$', '女$'), variable.name = 'variable', value.name = c('合计', '男', '女'), variable.factor = FALSE ) age.group = data.table( variable = as.character(c(1:22)), age_group = c( '0岁', '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁', '80-84岁', '85-89岁', '90-94岁', '95-99岁', '100岁及以上' ) ) data2 <- age.group[data2, on = .(variable)] data2 <- melt( data2, id.vars = c('year', 'type', 'area', 'age_group'), measure.vars = c('合计', '男', '女'), variable.name = 'gender', variable.factor = FALSE, value.name = 'value2' ) # 6 各地区分年龄、性别的人口 data6 <- as.data.table(data6) data6 <- melt( data6[, -c('合计', '男', '女')], id.vars = c('year', 'type', 'area'), measure.vars = patterns('计$', '男$', '女$'), variable.name = 'variable', value.name = c('合计', '男', '女'), variable.factor = FALSE ) data6 <- age.group[data6, on = .(variable)] data6 <- melt( data6, id.vars = c('year', 'type', 'area', 'age_group'), measure.vars = c('合计', '男', '女'), variable.name = 'gender', variable.factor = FALSE, value.name = 'value6' ) data.agegroup <- data6[data2, on = c("year", "type", "area", "gender", "age_group")] ############################## # 5 全国分年龄、性别的死亡人口状况 data.age <- as.data.table(data5) colnames(data.age) <- c( 'year', 'type', 'age', 'population_all', 'population_m', 'population_f', 'dead_all', 'dead_m', 'dead_f', 'dead_rate_all', 'dead_rate_m', 'dead_rate_f' ) rm(data5)
在这份整理好的死亡人口数据中,一共出现了这样8个基础维度,年份、城乡、区域、性别等4个维度基本上是每个表都有的,月份、年龄、受教育程度、婚姻状况等4个维度每一个分别与前四个组合起来得到一张表,但是没有月份、年龄、受教育程度、婚姻状况之间两两组合的数据。由于探索月份、受教育程度、婚姻状况都无所得,所以本文实际并未涉及这三个维度。
- 年份(year),三个年份分别是1999.11.1-2000.10.31、2009.11.1-2010.10.31、2019.11.1-2020.10.31。
- 城乡(type),分为不分城乡、城市、镇、乡村。
- 区域(area),分为全国以及各省份、直辖市、自治地区。
- 性别(gender),分为男、女。
- 年龄(age/age_group),分为0岁、1-4岁……95-99岁、100岁及以上等年龄段,也有按每一具体年龄的。
数据重塑完成后得到如下两个表:
- data.age:含有这些字段。
- year(年份)
- type(城乡)
- age(年龄、年龄段),其中既包含年龄段也包含每一个具体年龄数字。
- population_all(平均人口-合计)
- population_m(平均人口-男)
- population_f(平均人口-女)
- dead_all(死亡人口-合计)
- dead_m(死亡人口-男)
- dead_f(死亡人口-女)
- dead_rate_all(死亡率-合计)
- dead_rate_m(死亡率-男)
- dead_rate_f(死亡率-女)
- data.agegroup:含有这些字段。
- year(年份)
- type(城乡)
- area(区域)
- gender(性别)
- age_group(年龄段)
- value6(按年份、城乡、区域、性别、年龄段的总人口数)
- value2(按年份、城乡、区域、性别、年龄段的死亡人口数)。
3. 0岁人口的死亡人口数变化情况 🔗
现在有三个年份的数据,在最开始感到茫然又无所适从时,可以先从按年份看变动趋势开始进行探索。探索的过程中自然是需要将数据转换成图形来进行观察,由于之前刚刚学习了 ggplot2 的一点皮毛,本文用 ggplot2 来绘图。当图形中出现一些令人诧异的情形时,往往也需要查看原始数据,因此也使用 DT 包来查看具体数据。遇到图例项很多,需要弄清楚具体细节的情况,也会用 echarts4r 来绘制动态交互图形。
由于人口死亡率总是随年龄而递增的,因此本小节在绘图时更关注死亡人口数,同时也在图形之外关注人口死亡率的数据。按三个年份来看死亡人口数,数量上是递增的。在1999.11.1-2000.10.31到2009.11.1-2010.10.31再到2019.11.1-2020.10.31这三个统计期内,死亡人口数由731万–>742万–>796万,同时统计期内总的平均人口数由12.35亿–>13.30亿–>14.08亿,死亡率(千分率)的变化是5.92–>5.58–>5.66。从这里看起来,并未发现有什么需要关注的异常。
点击查看绘图的 R 代码
data.age[type == '不分城乡' & age == '总计',] |> ggplot(mapping = aes(x = year, y = dead_all, fill = year)) + geom_bar(stat = 'identity') + theme_classic() + labs(x = '年份', y = '死亡人口数', fill = '年份')
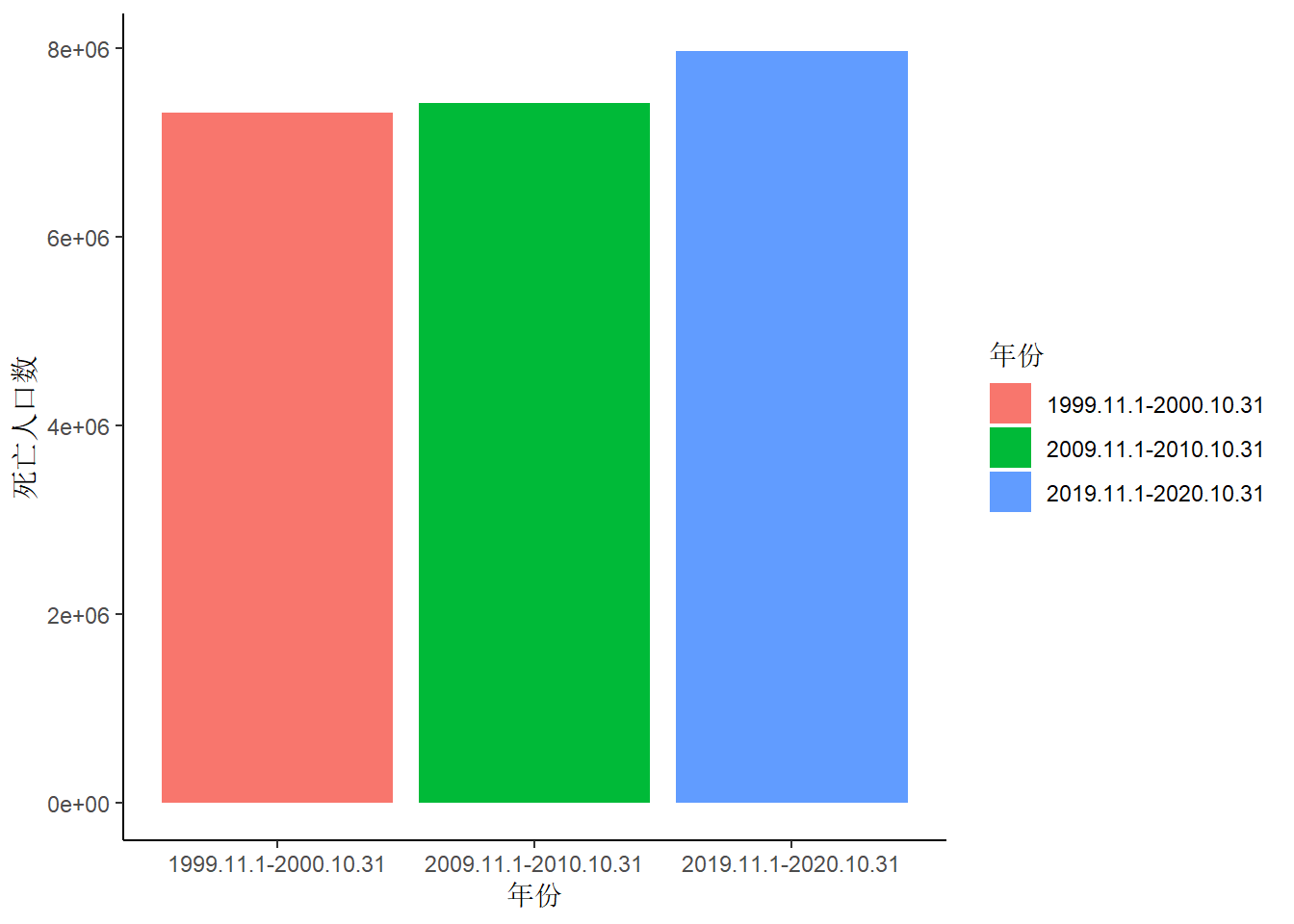
接着拆分城乡类型来看各年份的死亡人口数变化情况,城市、镇的死亡人口数递增,乡村的死亡人口数递减。由于我们国家近二十几年的城镇化率是不断提升的,人口由乡村流入城镇,因此单看城市、镇、乡村的死亡人口数变化趋势,也仍然是符合规律的。但却有一点值得注意,在上一次解读出生人口数据时,已知2010年的城镇乡村人口比例为45:55,至2020年上升至68:32,在这样的时代背景下,乡村的死亡人口数仍是超过城镇死亡人口数的。很显然,乡村人口的死亡率是高于城镇人口的。以2019.11.1-2020.10.31这个统计期为例,城市人口死亡率为3.62,镇人口死亡率为5.03,乡村人口死亡率为8.35。造成这么大差异的影响因素先放一放,继续向下探索。
点击查看绘图的 R 代码
# 由于 type 字段会被显示成 城市-乡村-镇 的顺序,这里对顺序做调整 data.age[type %in% c('城市', '镇', '乡村') & age == '总计',][, ':='(type_new = factor(type, levels = c('城市', '镇', '乡村')))] |> ggplot(mapping = aes(x = year, y = dead_all, fill = type_new)) + geom_bar(stat = 'identity', position = 'dodge') + theme_classic() + labs(x = '年份', y = '死亡人口数', fill = '城乡类型')
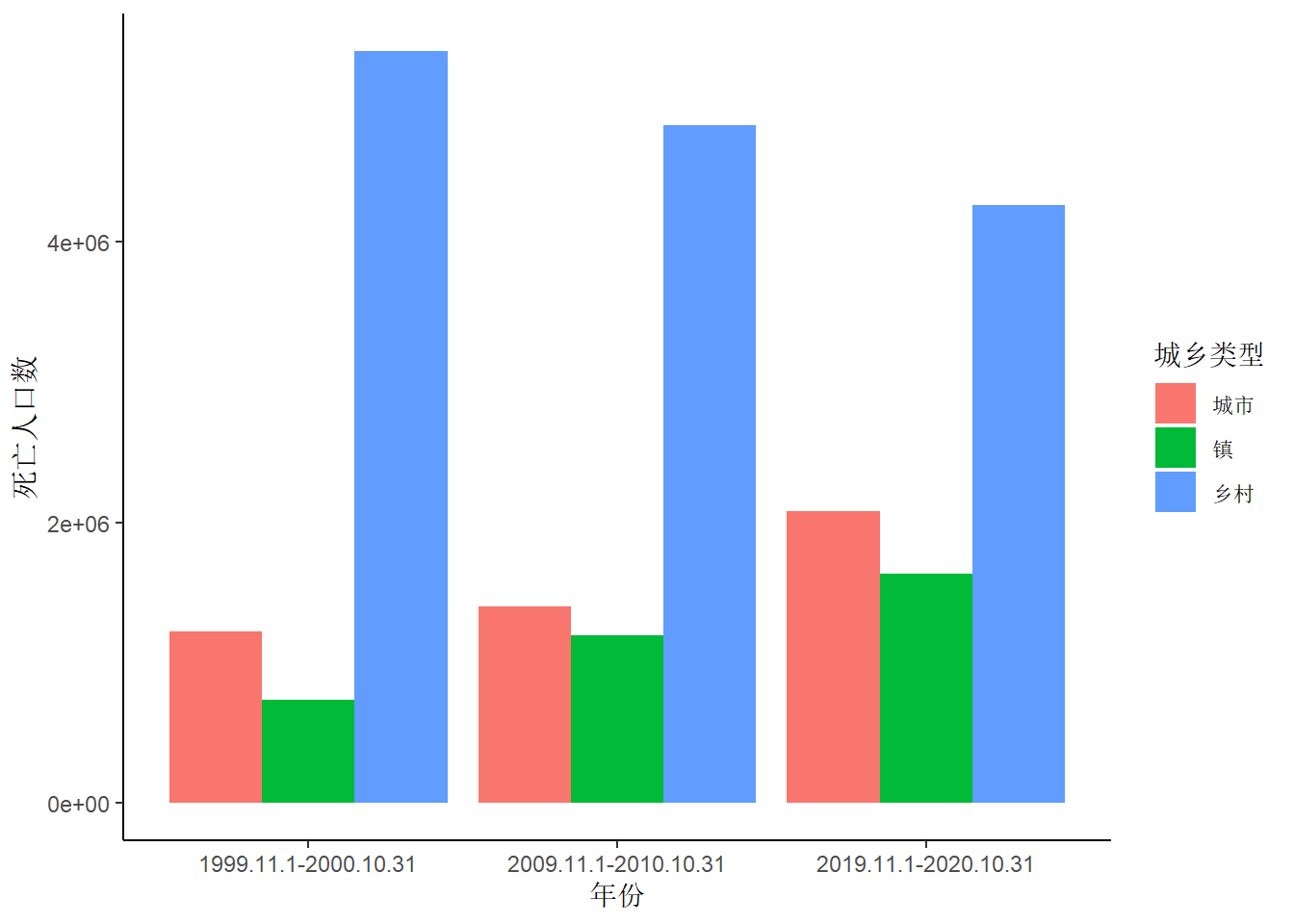
在按照年份、城乡类型统计死亡人口数的基础上,进一步按年龄段划分。下图中,有一个柱子高得出奇,即统计期为1999.11.1-2000.10.31的0-4岁的乡村人口死亡人数。在1999.11.1-2000.10.31到2009.11.1-2010.10.31再到2019.11.1-2020.10.31这三个统计期内,在0-4岁人口中,城市人口的死亡率是2.32–>0.74–>0.25,镇人口的死亡率是3.72–>0.88->0.38,乡村人口的死亡率是7.5–>1.63–>0.78。
点击查看绘图的 R 代码
# 由于 年龄段和城乡类型这两个字段在图例中的顺序不对,所以需要进行调整 data.age[type %in% c('城市', '镇', '乡村') & age %like% ".岁" , ][, ':='(age_new = factor( age, levels = c( '0-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁', '80-84岁', '85-89岁', '90-94岁', '95-99岁', '100岁及以上' ) ), type_new = factor(type, levels = c('城市', '镇', '乡村')))] |> ggplot(mapping = aes(x = year, y = dead_all, fill = age_new)) + geom_bar(stat = 'identity', position = 'dodge') + theme_classic() + labs(x = '年份', y = '死亡人口数', fill = '年龄段') + facet_wrap(vars(type_new), nrow = 3)
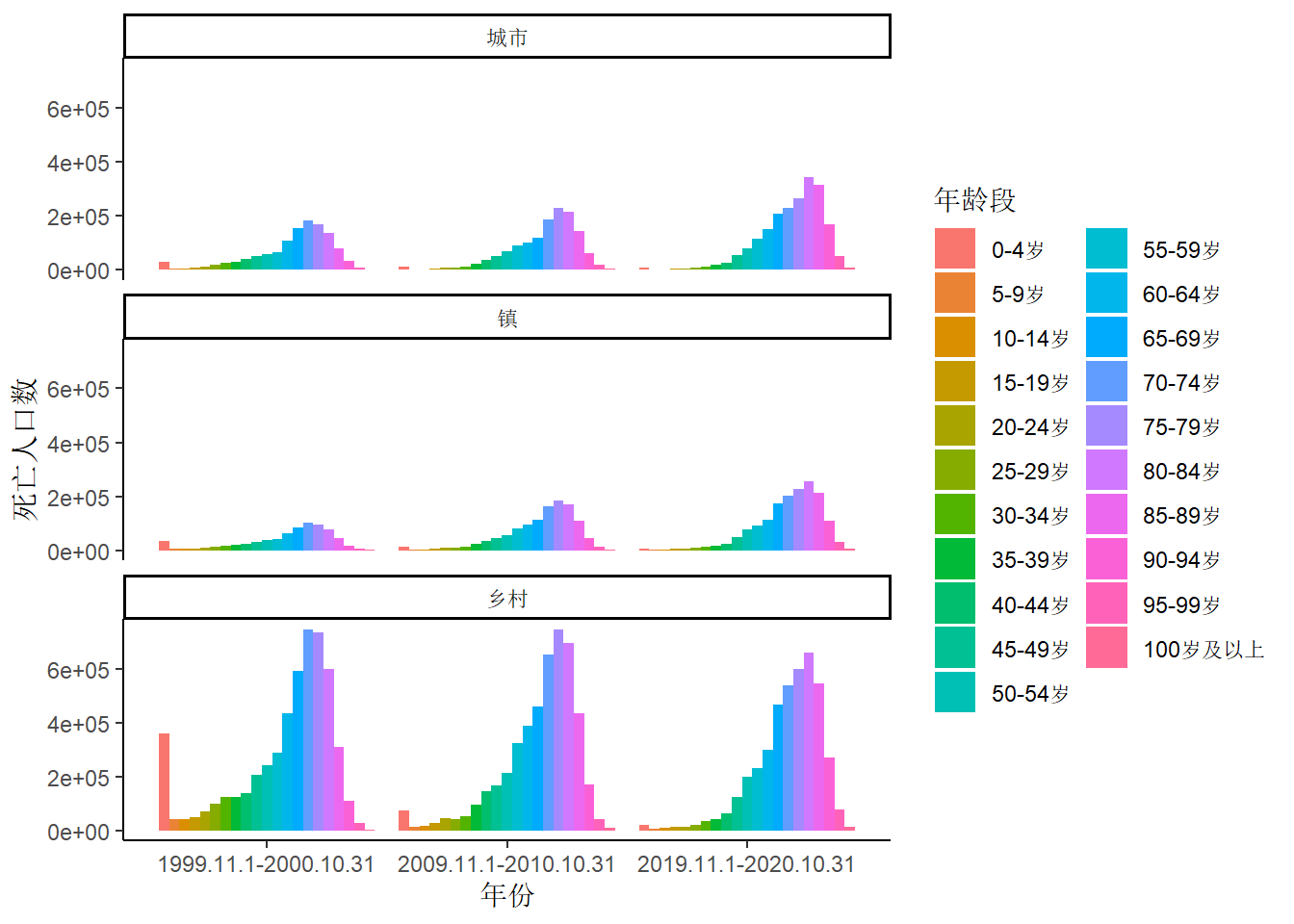
再进一步将年龄段细化为0-99岁,可以看到高得出奇的柱子其实是“0岁”。在1999.11.1-2000.10.31到2009.11.1-2010.10.31再到2019.11.1-2020.10.31这三个统计期内,仅观察0岁人口,城市人口的死亡率是9.58–>2.42–>0.89,镇人口的死亡率是16.77–>2.61->1.27,乡村人口的死亡率是34.08–>4.69–>2.4。由于下图图例项太多,这里不应过度关注细节,故隐去,但仍需知晓的是柱状图上的柱子从左到右是0到99岁。除了最左边的“0岁”,还有一点值得引起注意的是,0-99个连续的柱子中有一个“缺口”,这一点以后再展开。
点击查看绘图的 R 代码
data.age[type %in% c('城市', '镇', '乡村') & age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)), type_new = factor(type, levels = c('城市', '镇', '乡村')))] |> ggplot(mapping = aes(x = year, y = dead_all, fill = age_new2)) + geom_bar(stat = 'identity', position = 'dodge') + theme_classic() + theme(legend.position = 'none') + labs(x = '年份', y = '死亡人口数', fill = '年龄') + facet_wrap(vars(type_new), nrow = 3)
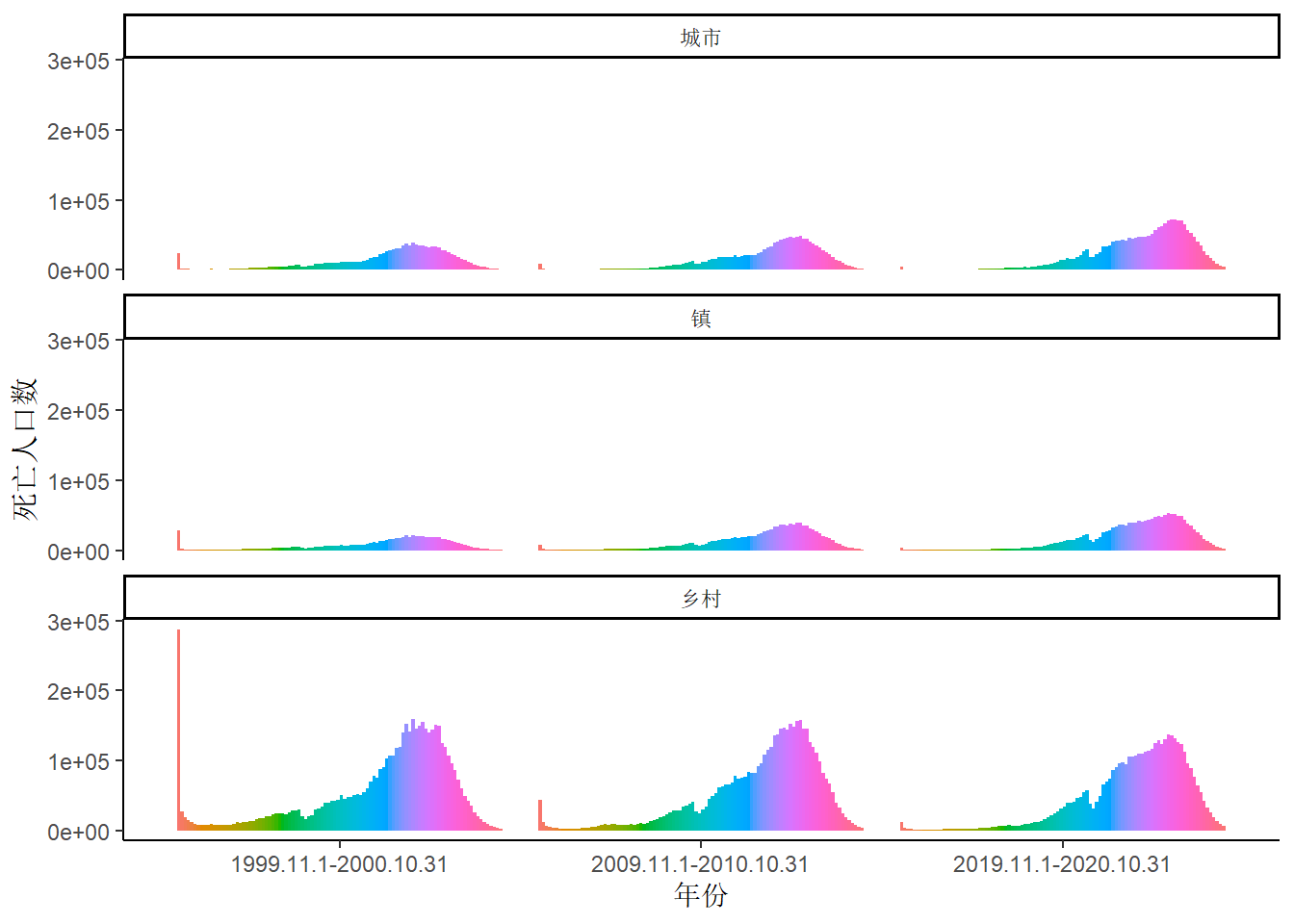
将以上探索的内容汇总在一处,可知尽管从全国范围上看人口死亡率似乎是变化不大,但若区分城市、镇、乡村来看,按死亡率来排序总是乡村 > 镇 > 城市。由于代表0岁人口的柱子出奇地高,观察到不论城市、镇、乡村,0岁人口死亡率是随时间下降较多的。
| 年份/人口死亡率 | 全国 | 城市 | 镇 | 乡村 | 全国(0岁) | 城市(0岁) | 镇(0岁) | 乡村(0岁) |
|---|---|---|---|---|---|---|---|---|
| 2000(1999.11.1-2000.10.31) | 5.92 | 4.21 | 4.45 | 6.87 | 26.9 | 9.58 | 16.77 | 34.08 |
| 2010(2009.11.1-2010.10.31) | 5.58 | 3.47 | 4.49 | 7.03 | 3.82 | 2.42 | 2.61 | 4.69 |
| 2020(2019.11.1-2020.10.31) | 5.66 | 3.62 | 5.03 | 8.35 | 1.53 | 0.89 | 1.27 | 2.4 |
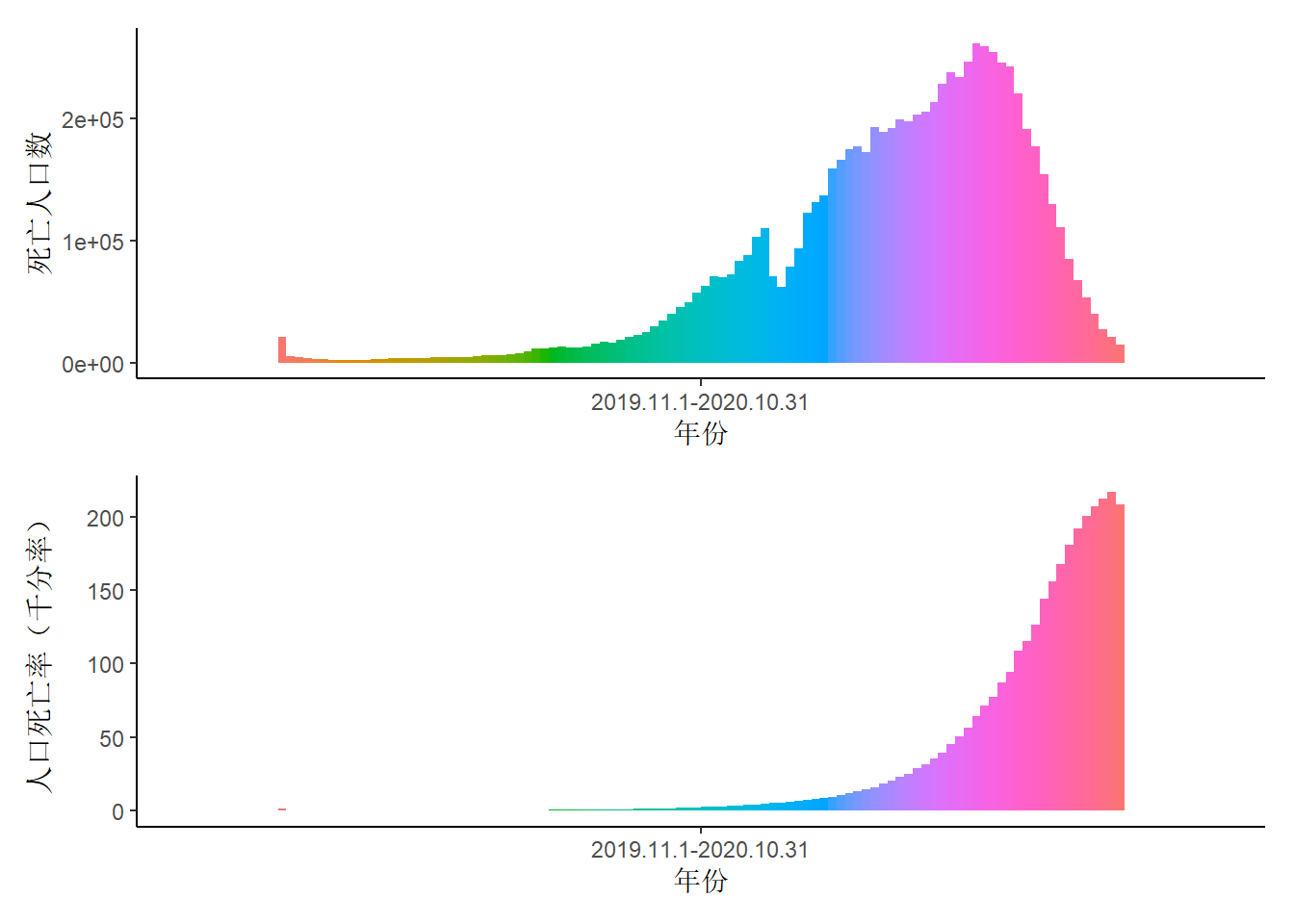
4. 一个缺口 🔗
单看2020(2019.11.1-2020.10.31)的数据,柱状图上死亡人口数的缺口出现在58-61岁3,而人口死亡率的柱状图对应位置上并未出现类似缺口,这说明58-61岁的总人口数就是少于相近年龄总人口数的。在2020年的58-61岁人群对应的出生年份是1959-1962年,造成这部分人群总人口数低的原因可能有两点。
- 一是在1959-1962年出生的人口数本身就少于相近年份;
- 二是在1959-1962年出生的人口存活至2020年的比例低于相近年份。
需要说明的是,下图中也去掉了数量较大的图例项,柱状图从左到右依次是0-99岁。
点击查看绘图的 R 代码
library(patchwork) p1 <- data.age[type == '不分城乡' & year == '2019.11.1-2020.10.31' & age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)))] |> ggplot(mapping = aes(x = year, y = dead_all, fill = age_new2)) + geom_bar(stat = 'identity', position = 'dodge') + theme_classic() + theme(legend.position = 'none') + labs(x = '年份', y = '死亡人口数', fill = '年龄') p2 <- data.age[type == '不分城乡' & year == '2019.11.1-2020.10.31' & age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)))] |> ggplot(mapping = aes(x = year, y = dead_rate_all, fill = age_new2)) + geom_bar(stat = 'identity', position = 'dodge') + theme_classic() + theme(legend.position = 'none') + labs(x = '年份', y = '人口死亡率(千分率)', fill = '年龄') p1 / p2
5. 死亡率的地域差异 🔗
经过一番维度组合的机械探索后,可以观察到一些十分浅显的表象,比如下面这些。
- 按月份观察死亡人口数,三个年份的数据均在10月份出现一个峰值,划分了城市、镇、乡村后再看此规律依然存在。
- 按受教育程度观察死亡率,“未上过学”和“小学”的人口死亡率最高。
- 按婚姻状况观察死亡率,“丧偶”的人口死亡率最高。
- 按区域对人口死亡率排序,也能得到排名靠前和靠后的区域。
但是!以上这些维度中,没有包含年龄或年龄段,而与死亡率最息息相关的显然是人的年龄。尽管“十月”、“未上过学”、“小学”、“丧偶”这些类别下人口死亡率相对较高,可是由于数据有限,无从得知这些类别下的人群年龄分布情况。因此,本小节将对死亡率的探索范围缩小至不同年龄段的地域差异。数据中与地域相关的维度有两个,一是城乡类型,即城市、镇、乡村;二是区域,即各省份、直辖市、自治区。为便于比对差异,将城乡类型和性别合并为一个新的组别,将城市和镇合并为城镇后,新的组别下有四个类别,分别是“城镇-男性”、“城镇-女性”、“乡村-男性”、“乡村-女性”。
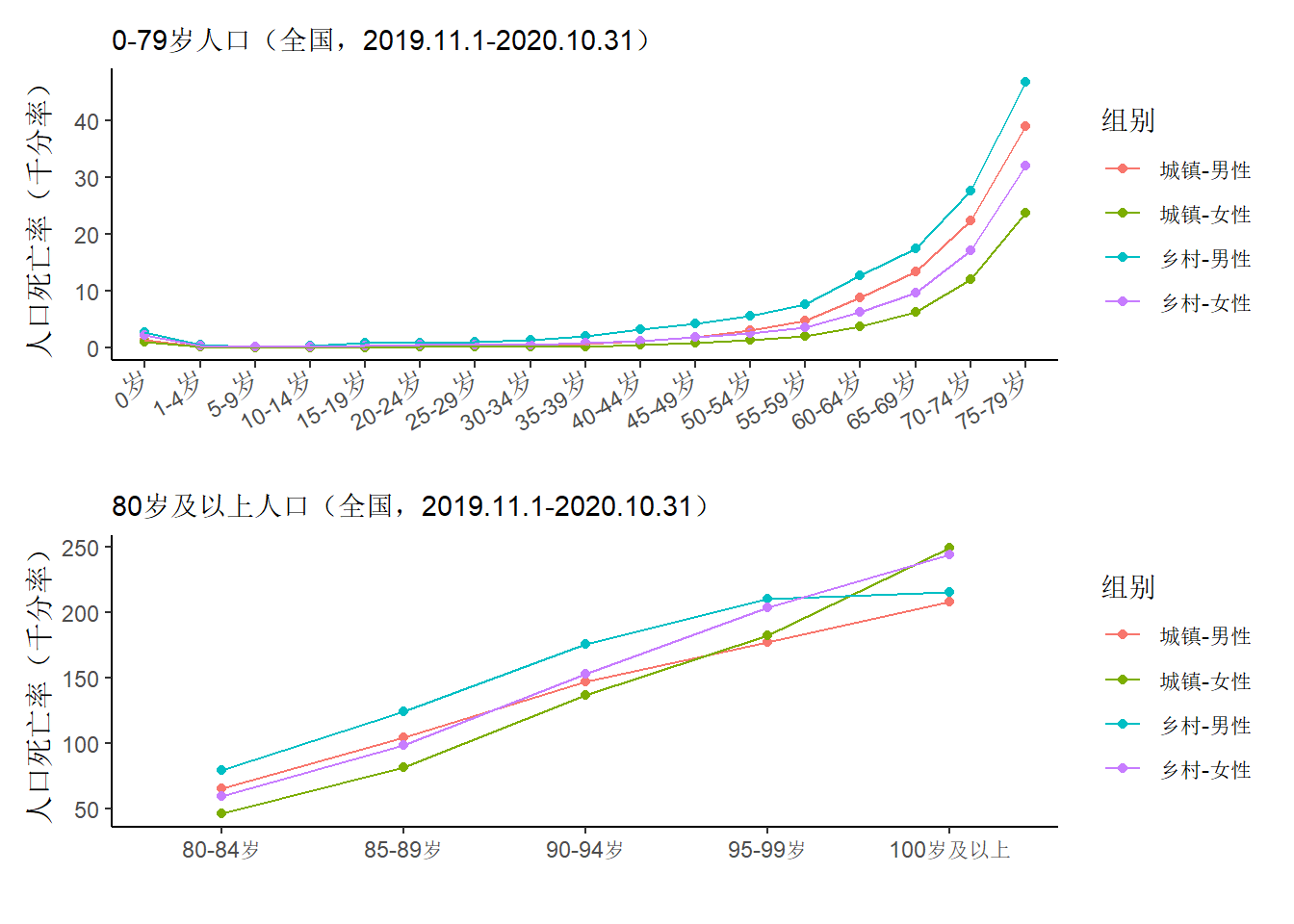
观察在2020年(2019.11.1-2020.10.31)全国所有年龄段的人口死亡率,由于0-79岁与80岁及以上的人口死亡率相差倍数极大,这里将其拆开绘制成两个独立的图形。如下图所示,在0-79岁人群中,从0岁到1-4岁,人口死亡率存在下降趋势,此后随着年龄增加,四个类别之间的差异逐渐变得清晰,按死亡率由高到底排序可以得到'乡村-男性' > '城镇-男性' > '乡村-女性' > '城镇-女性'。而在80岁及以上人群中,这个规律并不总是成立。由此,本节将全部年龄段拆成0岁、1-79岁、80岁及以上三个部分来进行探索。
点击查看绘图的 R 代码
data.agegroup$type_new <- ifelse( data.agegroup$type %in% c('城市', '镇') & data.agegroup$gender == '男', '城镇-男性', ifelse( data.agegroup$type %in% c('城市', '镇') & data.agegroup$gender == '女', '城镇-女性', ifelse( data.agegroup$type == '乡村' & data.agegroup$gender == '男', '乡村-男性', ifelse(data.agegroup$type == '乡村' & data.agegroup$gender == '女','乡村-女性', '其他') ) ) ) data.agegroup.new <- data.agegroup[type_new %in% c('城镇-男性', '城镇-女性', '乡村-男性', '乡村-女性') , by = .(year, area, type_new, age_group), .(value2 = sum(value2), value6 = sum(value6))][, ':='(dead_rate = round(value2 / value6, 5) *1000)] library(patchwork) p1 <- data.agegroup.new[year == '2019.11.1-2020.10.31' & area == '全国' & !age_group %in% c('80-84岁', '85-89岁', '90-94岁', '95-99岁', '100岁及以上'), ][, ':='(age_group_new = factor( age_group, levels = c( '0岁', '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁' ) ))] |> ggplot(mapping = aes( x = age_group_new, y = dead_rate, group = type_new, colour = type_new)) + geom_point() + geom_line() + theme_classic() + theme(axis.text.x = element_text(angle = 30, hjust = 1)) + labs( x = '', y = '人口死亡率(千分率)', subtitle = '0-79岁人口(全国,2019.11.1-2020.10.31)', colour = '组别') p2 <- data.agegroup.new[year == '2019.11.1-2020.10.31' & area == '全国' & age_group %in% c('80-84岁', '85-89岁', '90-94岁', '95-99岁', '100岁及以上'), ][, ':='(age_group_new = factor( age_group, levels = c('80-84岁', '85-89岁', '90-94岁', '95-99岁', '100岁及以上') ))] |> ggplot(mapping = aes( x = age_group_new, y = dead_rate, group = type_new, colour = type_new)) + geom_point() + geom_line() + theme_classic() + labs( x = '', y = '人口死亡率(千分率)', subtitle = '80岁及以上人口(全国,2019.11.1-2020.10.31)', colour = '组别') p1 / p2
5.1. 0岁人口 🔗
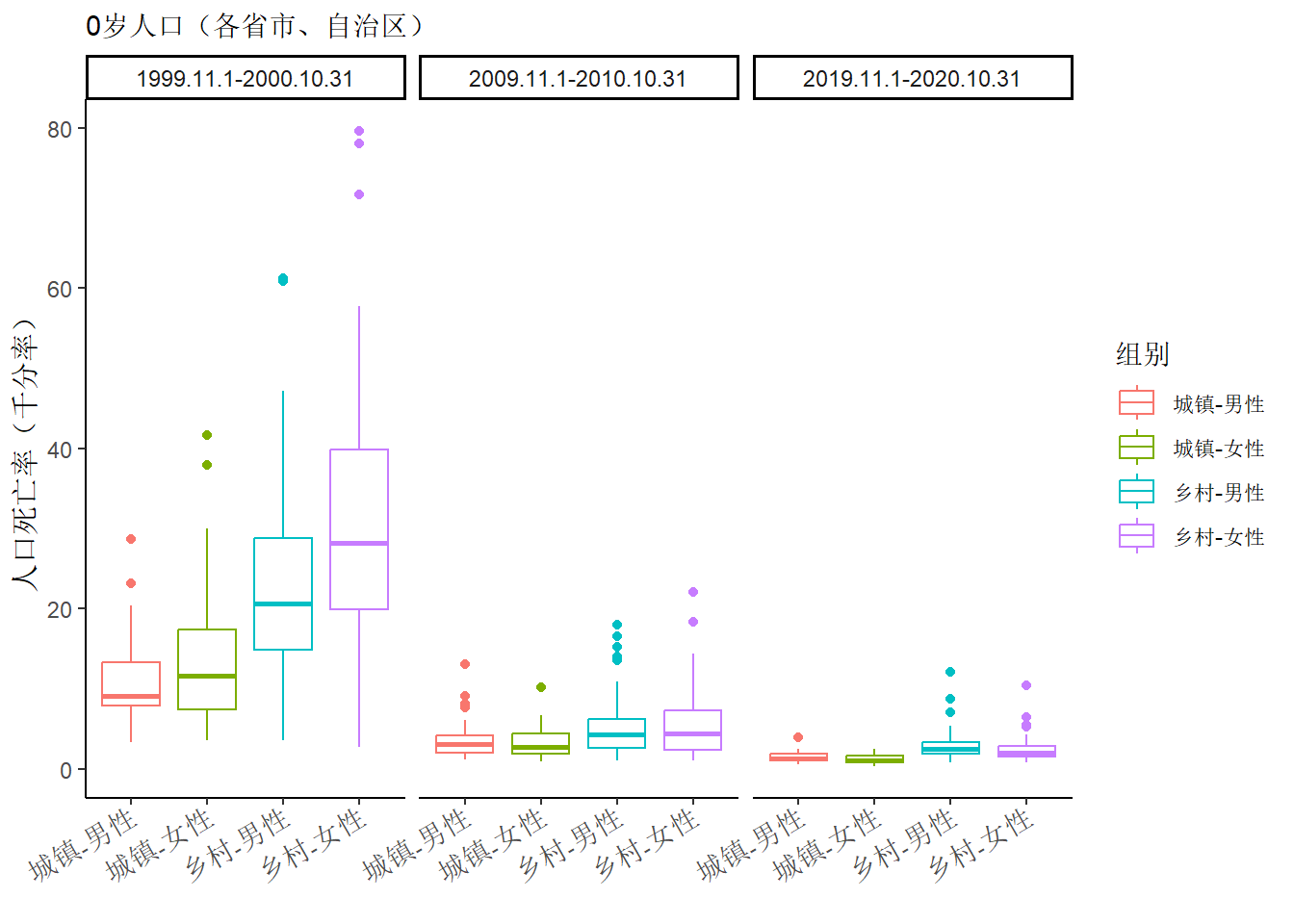
依时间顺序看,四个类别的0岁人口死亡率均有所下降,并且城镇与乡村之间、男性与女性之间的差异均在缩小。用箱线图能直接看出来的“差异缩小”在于均值、取值范围之间的差异缩小。基于此,仍需引起注意的是,到了2020年(2019.11.1-2020.10.31)“乡村-男性”和“乡村-女性”这两个类别仍然存在三个离群点。
点击查看绘图的 R 代码
data.agegroup.new[age_group %in% c('0岁')&!area=='全国', ] |> ggplot(mapping = aes( x = type_new, y = dead_rate, group = type_new, colour = type_new)) + geom_boxplot() + theme_classic() + facet_grid(cols = vars(year)) + labs( x = '', y = '人口死亡率(千分率)', subtitle = '0岁人口(各省市、自治区)', colour = '组别') + theme(axis.text.x = element_text(angle = 30, hjust = 1))
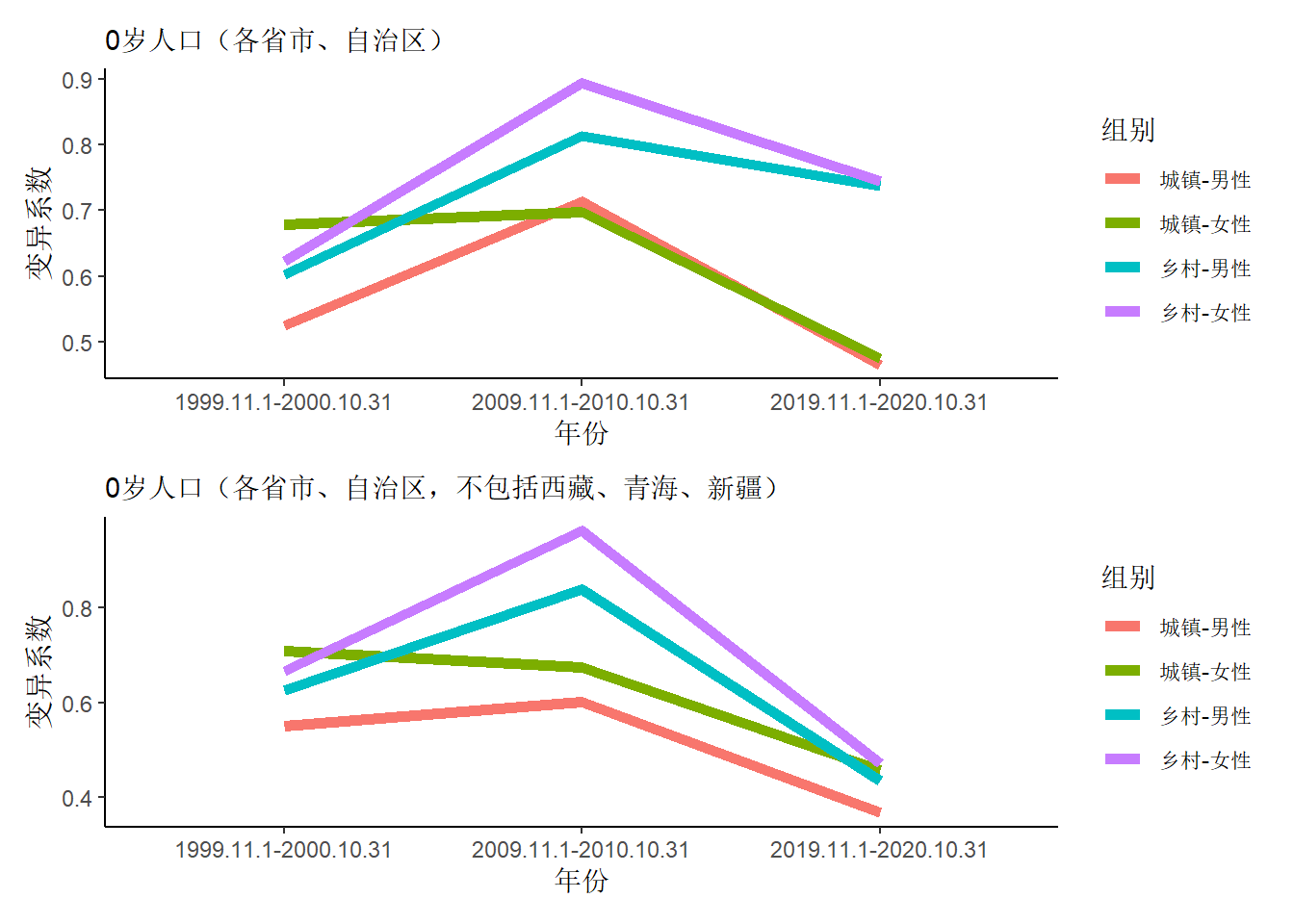
这里计算一下每个类别下人口死亡率的变异系数(标准差除以均值),用于衡量四类数据的离散程度。下面有两个图,均是分别绘制了四个类别的变异系数在三个年份的变化趋势,区别是上面的图在计算变异系数时包含了全国所有区域,而下面的图则是去掉了西藏、青海、新疆后再计算变异系数。只看上面的图,可以观察到两点:
- 在2000年(1999.11.1-2020.10.31),造成四个类别的人口死亡率离散程度存在差异的因素显然该是性别,按变异系数从大到小排序是
'城镇-女性' > '乡村-女性' > '乡村-男性' > '城镇-男性'。 - 到了2020年(2019.11.1-2020.10.31),城镇与乡村的差异替代了性别所造成的差异。
仅从这一个指标来看,似乎可以得到结论,20年的经济飞速发展使得城乡差异扩大了。但如果只看下面去掉三个离群点后再计算得到的图,似乎又可以得到另一个截然相反的结论。对比下面两个包含、去掉三个离群点的变异系数的折线图,探索到这里,说明该看看各个区域的具体数据了。
点击查看绘图的 R 代码
data <- data.agegroup.new[age_group %in% c('0岁') & !area == '全国', by = .(year, type_new), .(cv = sd(dead_rate) / mean(dead_rate))][order(type_new), ] p1 <- data |> ggplot(mapping = aes( x = year, y = cv, group = type_new, colour = type_new )) + geom_line(linewidth = 2) + theme_classic() + labs( x = '年份', y = '变异系数', subtitle = '0岁人口(各省市、自治区)', colour = '组别' ) data2 <- data.agegroup.new[age_group %in% c('0岁') & !area %in% c('全国', '西藏', '青海', '新疆'), by = .(year, type_new), .(cv = sd(dead_rate) / mean(dead_rate))][order(type_new), ] p2 <- data2 |> ggplot(mapping = aes( x = year, y = cv, group = type_new, colour = type_new )) + geom_line(linewidth = 2) + theme_classic() + labs( x = '年份', y = '变异系数', subtitle = '0岁人口(各省市、自治区,不包括西藏、青海、新疆)', colour = '组别' ) p1/p2
单独取2019.11.1-2020.10.31的0岁死亡人口数据来看,基于乡村医疗卫生条件整体比城镇差的常识,我们可以接受乡村的0岁人口死亡率整体上高于城镇的事实。下图中可以清楚看到在“乡村-男性”、“乡村-女性”这两个类别下,西藏、青海、新疆即原来箱线图中的三个离群点,比其他指标数值小的区域多出数倍的差异,并且西藏的0岁人口死亡率更是远高于其他区域。
点击查看绘图的 R 代码
data.agegroup.new[year == '2019.11.1-2020.10.31' & age_group == '0岁' & !area == '全国',] |> ggplot(mapping = aes(x = reorder(area, dead_rate), y = dead_rate)) + geom_bar( mapping = aes(fill = dead_rate), stat = 'identity', position = 'dodge' ) + coord_flip() + theme_classic() + geom_text( mapping = aes(label = dead_rate), size = 3, hjust = -0.1, stat = 'identity' ) + facet_grid(cols = vars(type_new)) + scale_y_continuous(breaks = c(0, 2, 6, 12)) + labs( x = '区域', y = '', fill = '人口死亡率', subtitle = '0岁人口(各省市、自治区,2019.11.1-2020.10.31)' ) + theme(axis.text.y = element_text( angle = 0, hjust = 1, size = 7.5 ))
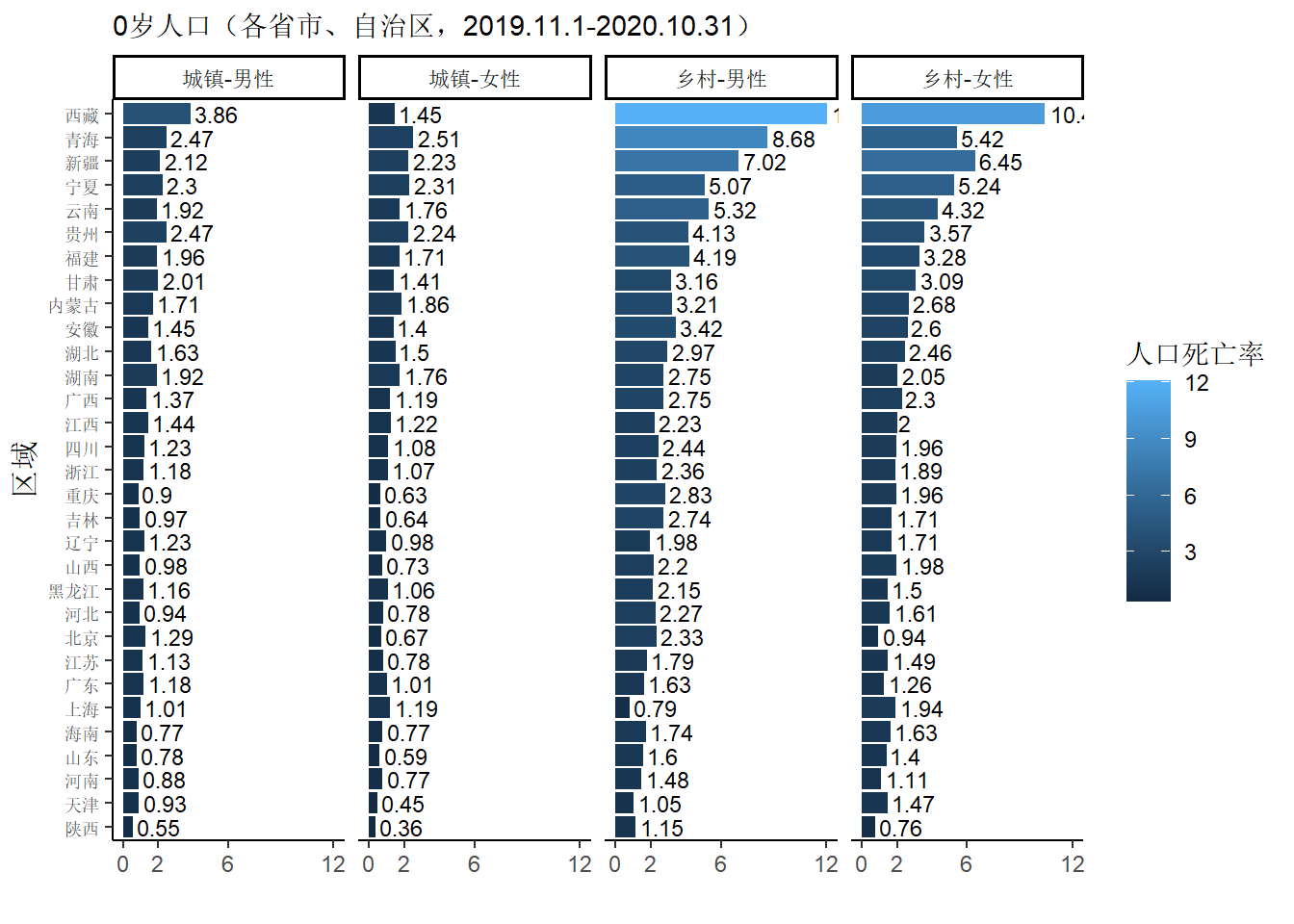
在国家卫健委官网能查看2011年至今的中国卫生健康统计年鉴,从2020年卫生统计年鉴中可以找到下表中的几个指标含义4,以及2019年的具体指标数值5。可以看到西藏乡村0岁人口死亡率高的背后,是乡村孕产妇死亡率也很高。当然,这些指标数据并不能解释原因,只是加深了一层表象,
| 区域 | 围产儿死亡率(‰) | 孕产妇建卡率 | 孕产妇死亡率(1/10万)-市级 | 孕产妇死亡率(1/10万)-县级 |
|---|---|---|---|---|
| 全国 | 4.02 | 92.4% | 8.9 | 11.8 |
| 西藏 | 12.64 | 66.8% | 17.7 | 68.8 |
5.2. 80岁及以上 🔗
在2000年、2010年、2020年的三次全国人口普查数据中,80岁及以上的高龄老年人口在总人口中占比极低,这个比例在升高,0.9%–>1.5%–>2.5%;而80岁及以上死亡人口在总死亡人口中占比较高,这个比例也在升高,19.9%–>28.8%–>38.5%;同时,80岁及以上人口的死亡率在下降,121–>101–>85。这三点共同说明了一个常识,我国国人的寿命延长了。
| 年份 | 总人口数 | 80岁及以上人口数 | 80岁及以上人口占比 | 死亡人口数 | 80岁及以上死亡人口数 | 80岁及以上死亡人口占比 | 死亡率(千分率) |
|---|---|---|---|---|---|---|---|
| 1999.11.1-2000.10.31 | 1242612226 | 11991083 | 0.9% | 7313081 | 1457832 | 19.9% | 121 |
| 2009.11.1-2010.10.31 | 1332810869 | 20989346 | 1.5% | 7421990 | 2138949 | 28.8% | 101 |
| 2019.11.1-2020.10.31 | 1409778724 | 35800835 | 2.5% | 7965772 | 3067715 | 38.5% | 85 |
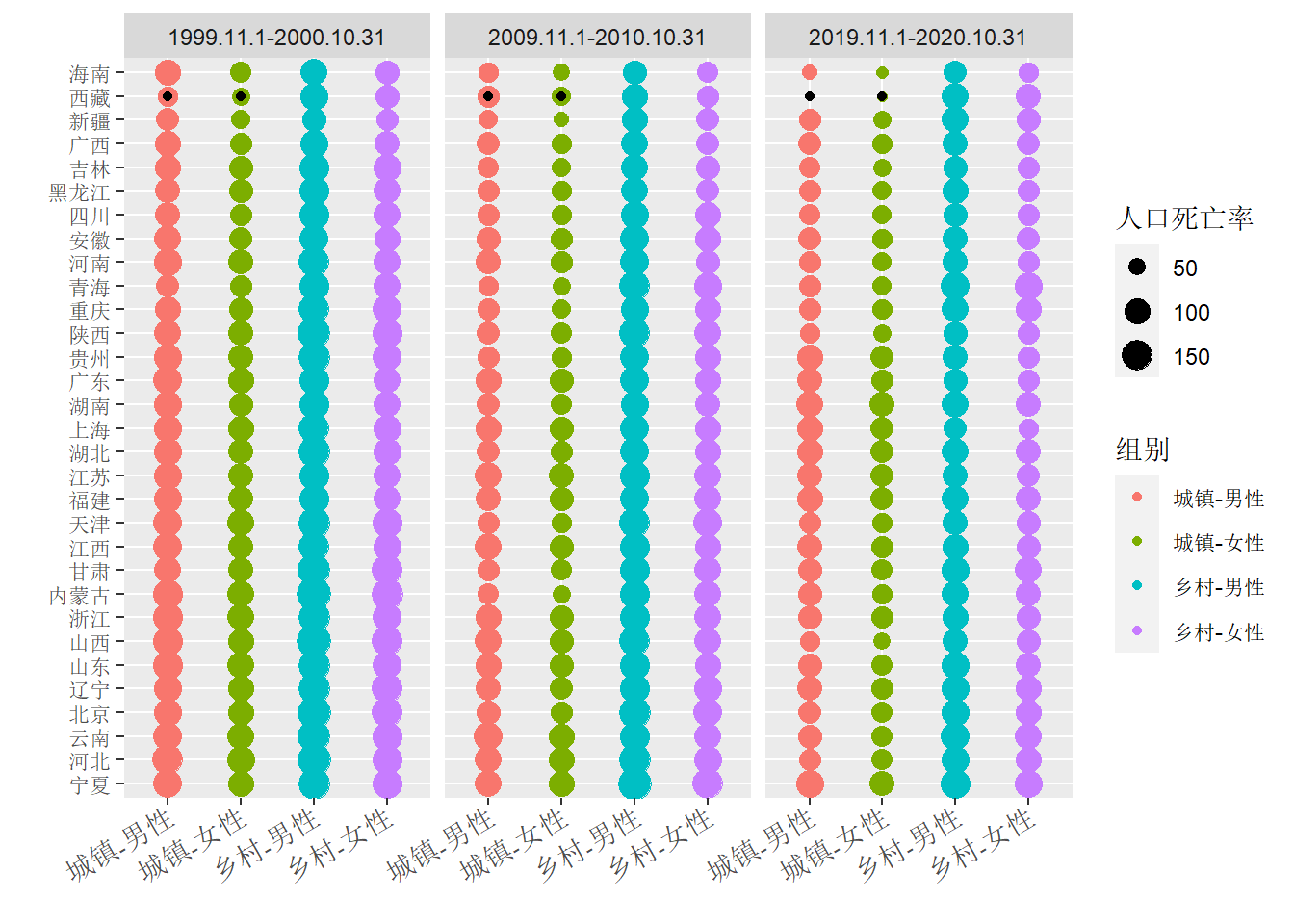
将80岁及以上人群的死亡率按年份、区域绘制成如下多列单轴散点图。令人感到意外的是在2020年(2019.11.1-2020.10.31),西藏、海南的“城镇-男性”、“城镇-女性”死亡率最低。
点击查看绘图的 R 代码
data <- data.agegroup.new[age_group %in% c('80-84岁', '85-89岁','90-94岁', '95-99岁','100岁及以上'), by = .(year, area, type_new), .(value2 = sum(value2), value6 = sum(value6))][,':='(dead_rate = round(value2 / value6, 5) * 1000)] # 单轴散点图 data[!area == '全国', ] |> ggplot(aes( x = type_new, y = reorder(area, dead_rate, decreasing = TRUE), size = dead_rate, colour = type_new )) + geom_point() + facet_grid(cols = vars(year)) + labs( x = '', y = '', colour = '组别', size = '人口死亡率' ) + theme(axis.text.x = element_text(angle = 30, hjust = 1)) + annotate( geom = "point", x = c('城镇-男性', '城镇-女性'), y = '西藏', color = 'black')
5.3. 1-79岁 🔗
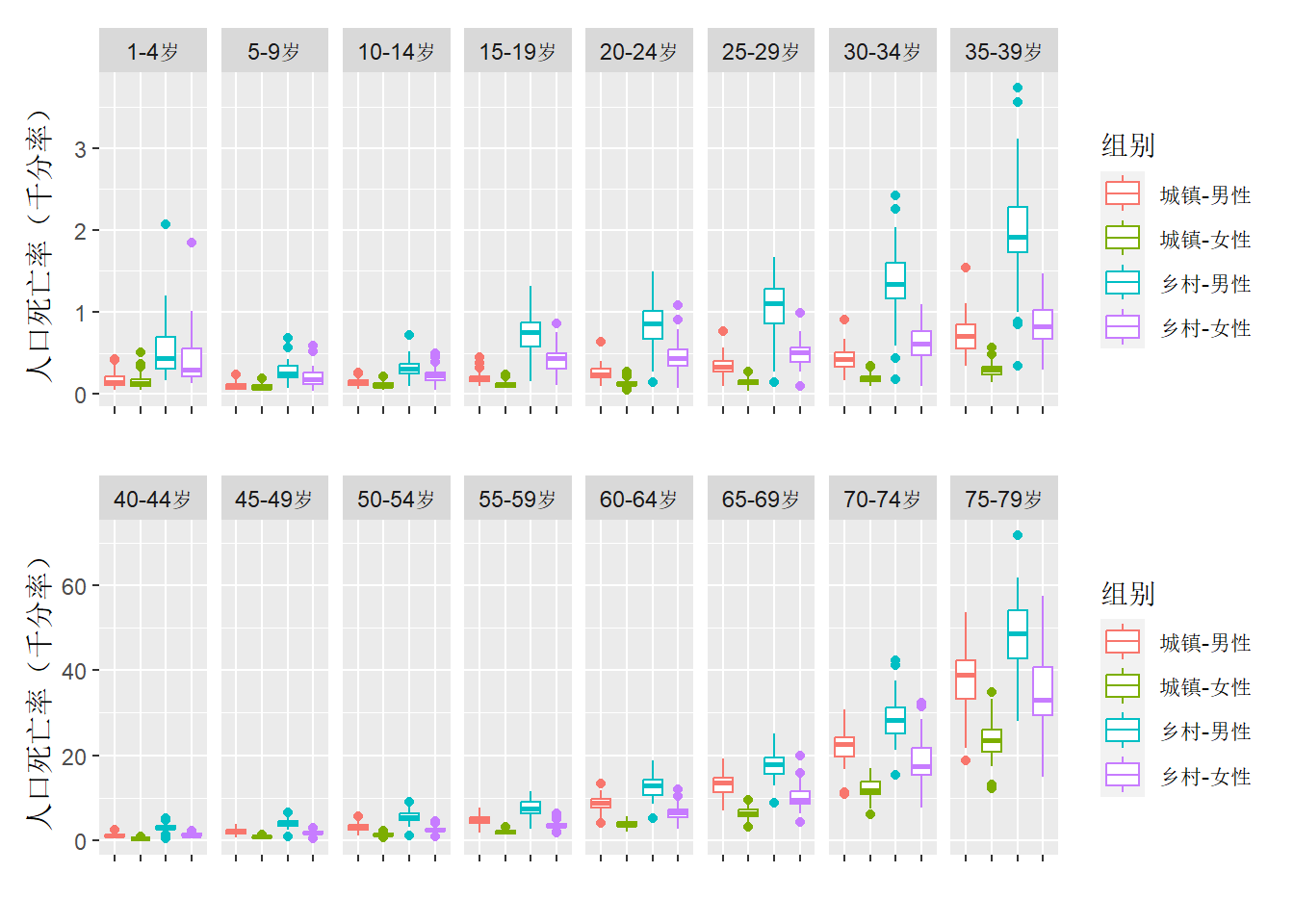
这里继续将视角由整体转向局部,由全国转移至全国各区域,相比于0岁人口的死亡率箱线图只存在超出上限的离群点,下图中1-79岁的各年龄段死亡率箱线图存在一些低于下限的离群点。通过翻查数据,可知这些离群点大多指向一个区域–上海。
点击查看绘图的 R 代码
p1 <- data.agegroup.new[year == '2019.11.1-2020.10.31' & age_group %in% c('1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁') & !area == '全国',][, ':='(age_group_new = factor( age_group, levels = c( '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁' ) ))] |> ggplot(mapping = aes(x = type_new, y = dead_rate, colour = type_new)) + geom_boxplot(position = 'dodge') + facet_grid(cols = vars(age_group_new)) + labs(x = '', y = '人口死亡率(千分率)', colour = '组别') + theme(axis.text.x = element_blank()) p2 <- data.agegroup.new[year == '2019.11.1-2020.10.31' & age_group %in% c('40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁') & !area == '全国', ][, ':='(age_group_new = factor( age_group, levels = c( '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁' ) ))] |> ggplot(mapping = aes(x = type_new, y = dead_rate, colour = type_new)) + geom_boxplot(position = 'dodge') + facet_grid(cols = vars(age_group_new)) + # theme_classic() + labs(x = '', y = '人口死亡率(千分率)', colour = '组别') + theme(axis.text.x = element_blank()) p1 / p2
下表展示了在2020年(2019.11.1-2020.10.31),1-79岁各年龄段、各类别下人口死亡率最低的区域。这里显然存在一个规律,在“乡村-男性”、“乡村-女性”这两个类别下,绝大多数年龄段死亡率最低的区域都是上海,而这个规律在另外两个年份也是成立的。在上一小节中,80岁及以上的“城镇-男性”、“城镇-女性”人口死亡率最低的区域是海南、西藏,而在1-79岁中年龄较大的人群中这个规律依然成立。
点击查看绘图的 R 代码
data <- data.agegroup.new[year == '2019.11.1-2020.10.31' & age_group %in% c('1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁') & !area == '全国',][, ':='(age_group_new = factor( age_group, levels = c( '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁' ) ))] #按照type_new,age_group分组,按照 dead_rate 排序并生成序号,取最小值,展示 data <- setDT(data)[order(dead_rate), rank_asc := 1:.N, by = .(type_new, age_group)] data1 <- data[rank_asc == 1, ] data1 <- dcast(data1, age_group_new ~ type_new, value.var = "area") colnames(data1)[1] <- "年龄段" DT::datatable(data1, options = list(dom = 't', pageLength = 21), caption = "2019.11.1-2020.10.31,1-79岁人口死亡率最低的区域")
5.4. 试试降维 🔗
在探索数据的时候,如果仅仅只是用一般的可视化图形进行探索,由于图形能展示的维度有限,所能展示内容的范围上也会被限定于对比绝对值或比例大小、变动趋势、数据分布、简单的变量关系等等。面对本文中多维度的面板数据,也可以试着先用一些多元统计分析的方法来做降维处理。比如用聚类来探索各区域之间的相似程度,或者借用因子分析中的因子得分图来观察各区域在不同年龄段的表现。
但是降维往往是作为一种在结果解读上目的性很强的分析方法。这篇文章写下来我心里有好几处疑惑,不过想着最初定调是不分析原因而先放下,所以这一小节在结果解读上也写得很浅。
5.4.1. 聚类 🔗
本小节聚类6使用的数据是在2019.11.1-2020.10.31的1-79岁人群的死亡率数据,聚类的样本是各个区域,计算样本之间距离的指标是各年龄段死亡率,使用系统聚类法,样本之间的距离默认使用欧式距离,类间距离使用平均距离法。
下图中聚类的数据范围限定于“乡村-男性”。在上一小节的探索中,已经知晓上海在绝大多数年龄段的死亡率都是最低,因而上海被单独聚为一类符合对数据的认知。
点击查看聚类的 R 代码
data.c1 <- dcast(data[type_new == '乡村-男性', ], area ~ age_group, value.var = "dead_rate") # data.table 格式的数据框无法被赋予行名,转换成data.frame data.c1 <- as.data.frame(data.c1) rownames(data.c1) <- data.c1$area # 对样本聚类 hc <- hclust(dist(data.c1[,-1]), method = "ave") # 判断聚类簇数,4的票数最多 # nc <- NbClust::NbClust(data.c1[, -1], min.nc = 2, max.nc = 15, method = "average") # table(nc$Best.nc[1, ]) # 计算聚类的评估指标,轮廓系数0.25 # sc <- cluster::silhouette(cutree(hc, k = 4), dist(data.c1[, -1])) # plot(sc) # 绘图 plot(hc, main = '2019.11.1-2020.10.31,1-79岁,乡村-男性', sub = '', xlab = '', ylab = '', cex = .8) rect.hclust(hc, k = 4, border = 'red')
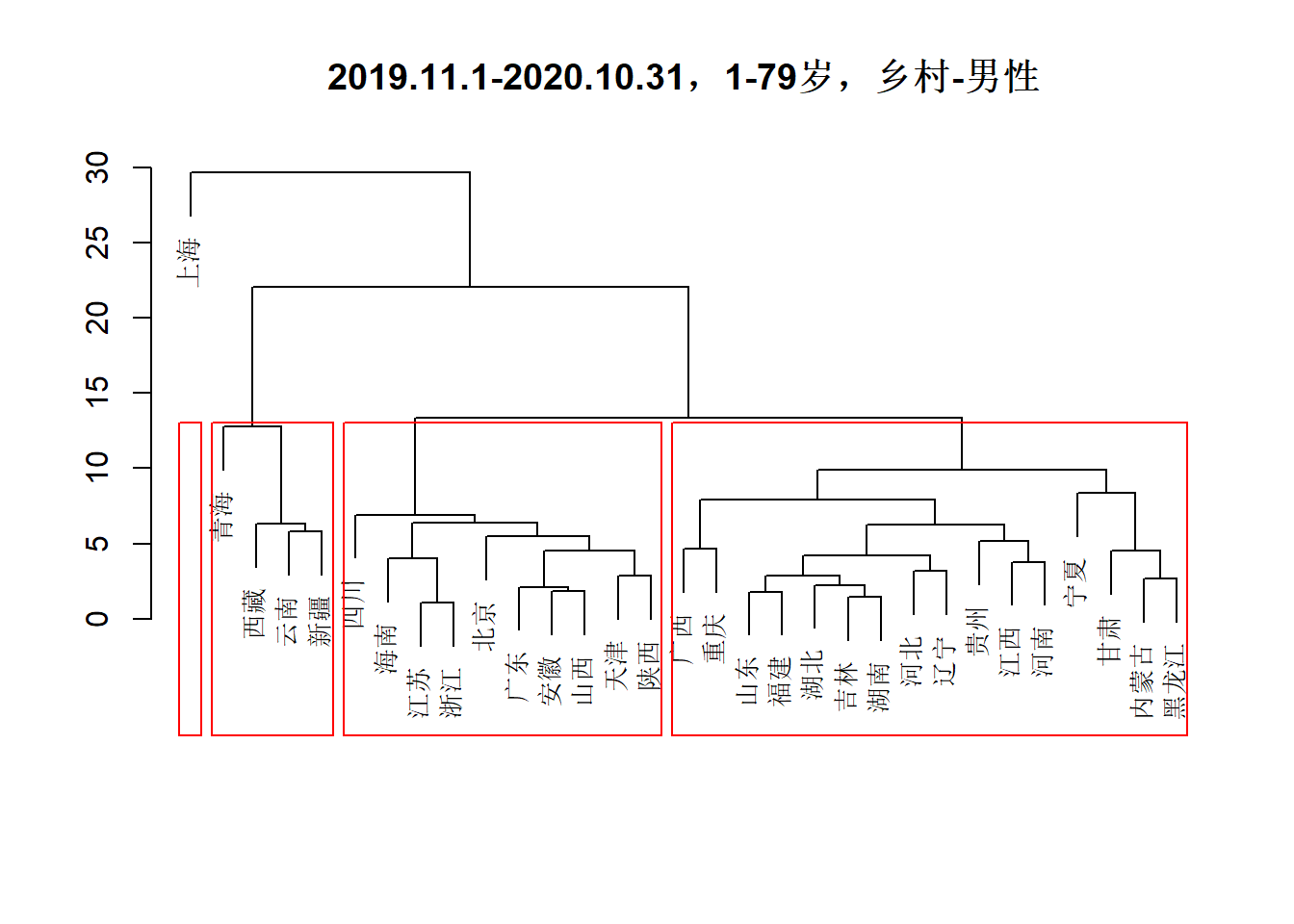
得到的四个类分别是:
- 类1:上海。
- 类2:云南、新疆、西藏、青海。
- 类3:内蒙古、吉林、宁夏、山东、广西、江西、河北、河南、湖北、湖南、甘肃、福建、贵州、辽宁、重庆、黑龙江。
- 类4:北京、四川、天津、安徽、山西、广东、江苏、浙江、海南、陕西。
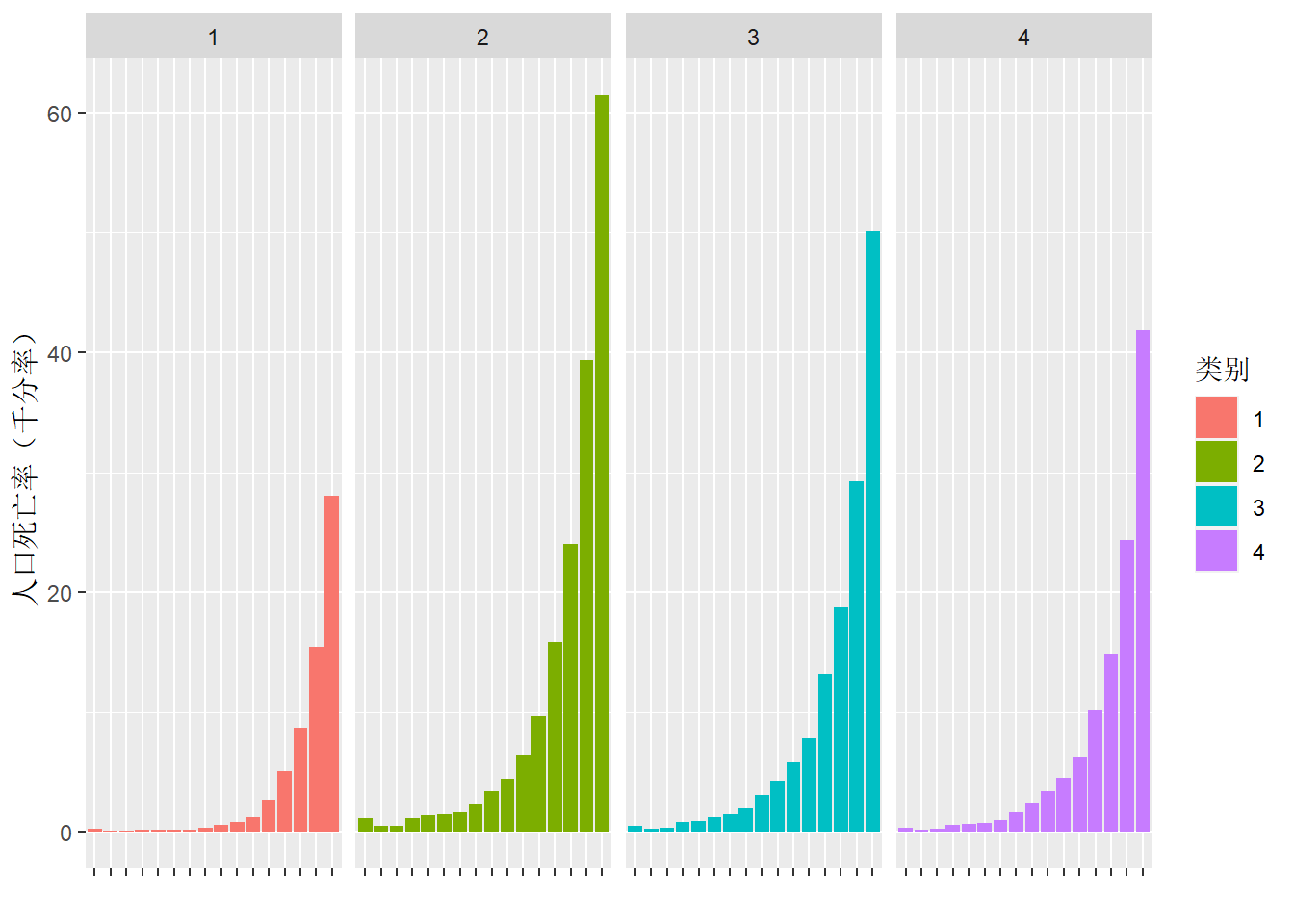
分别计算每个类中的样本在各年龄段的死亡率中位数,得到下图,类1-4可以看做死亡率极低、高、中、低等四类。
点击查看绘图的 R 代码
# 根据给定的高度或者类别数目切割树状图,返回一个向量,表示每个观测值所属的类别 cluster <- cutree(hc, k = 4) # 对数据按照给定的因子进行分组,并应用指定的函数 centers <- aggregate(data.c1[, -1], by = list(cluster), FUN = median) centers <- as.data.table(centers) centers.m <- melt(centers, id = 1) centers.m[, ':='( variable_new = factor( variable, levels = c( '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁')),group_new = factor(Group.1, levels = c(1, 2, 3, 4)))] |> ggplot(mapping = aes(x = variable_new, y = value, fill = group_new)) + geom_bar(stat = 'identity', position = 'dodge') + facet_grid(cols = vars(group_new)) + labs(x = '', y = '人口死亡率(千分率)', fill = '类别') + theme(axis.text.x = element_blank())
下图中聚类的数据范围限定于“乡村-女性”,和上图一样,也是上海被单独聚为一类。
点击查看聚类的 R 代码
data.c2 <- dcast(data[type_new == '乡村-女性', ], area ~ age_group, value.var = "dead_rate") # data.table 格式的数据框无法被赋予行名,转换成data.frame data.c2 <- as.data.frame(data.c2) rownames(data.c2) <- data.c2$area hc <- hclust(dist(data.c2[,-1]), method = "ave") # # 判断聚类簇数,4的票数最多 # nc <- NbClust::NbClust(data.c2[, -1], min.nc = 2, max.nc = 15, method = "average") # table(nc$Best.nc[1, ]) # # 计算聚类的评估指标,轮廓系数平均值0.47 # sc <- cluster::silhouette(cutree(hc, k = 4), dist(data.c2[, -1])) # plot(sc) # clusplot(pam(data.c2[, -1], 4)) plot(hc, main = '2019.11.1-2020.10.31,1-79岁,乡村-女性', sub = '', xlab = '', ylab = '', cex = .8) rect.hclust(hc, k = 4, border = 'red')
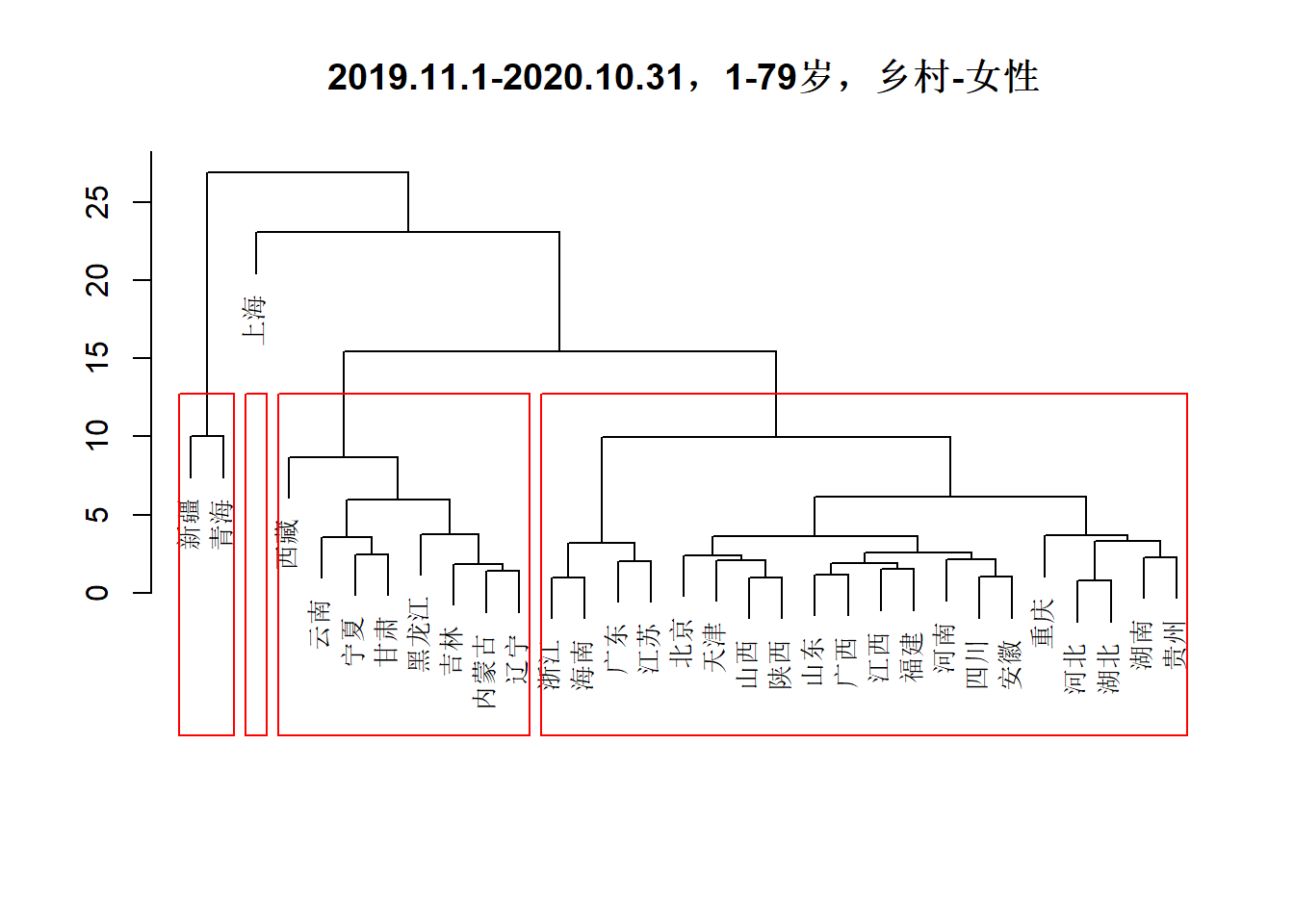
得到的四个类别分别是:
- 类1:上海
- 类2:云南、内蒙古、吉林、宁夏、甘肃、西藏、辽宁、黑龙江
- 类3:北京、四川、天津、安徽、山东、山西、广东、广西、江苏、江西、河北、河南、浙江、海南、湖北、湖南、福建、贵州、重庆、陕西
- 类4:新疆、青海
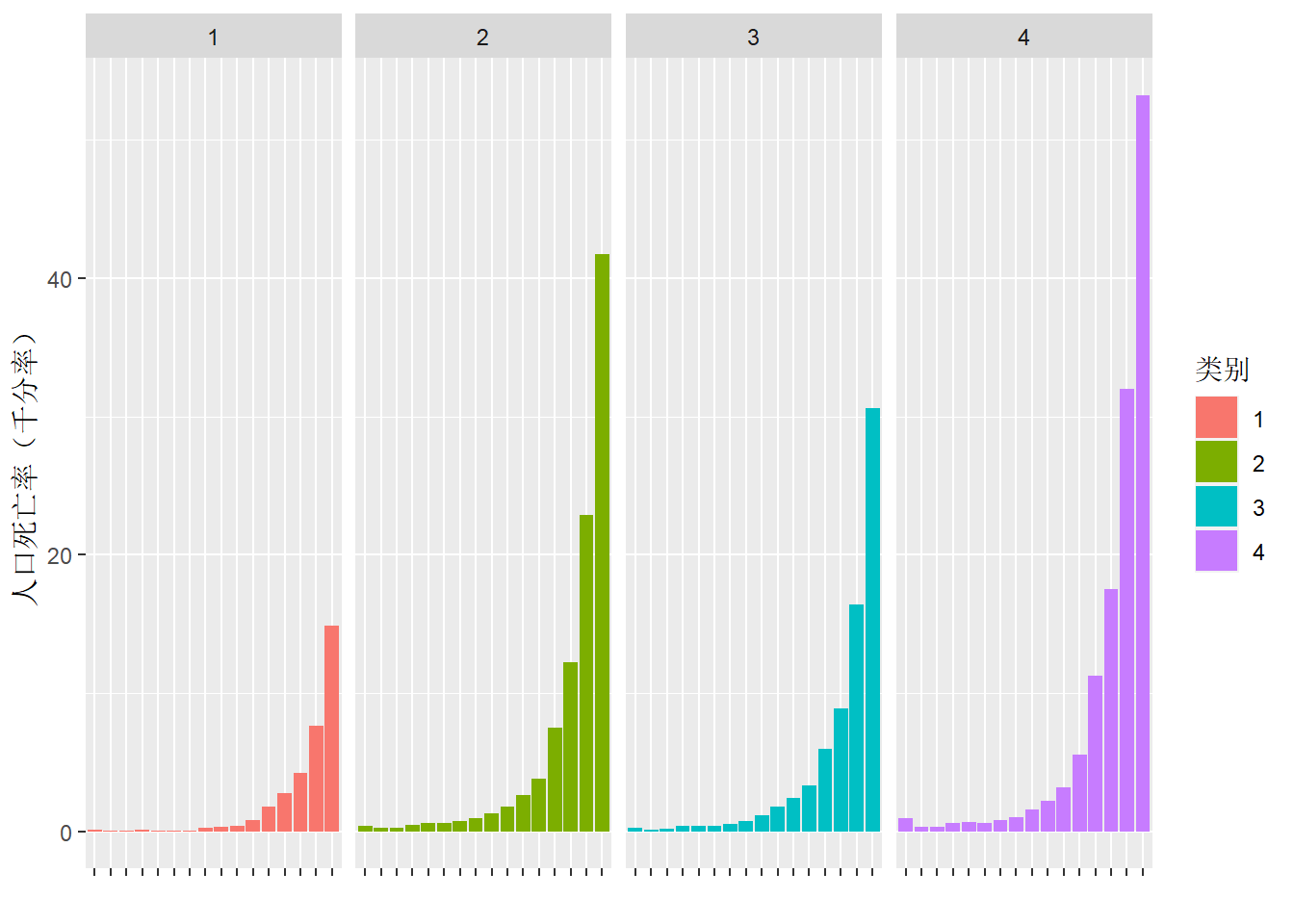
分别计算每个类中的样本在各年龄段的死亡率中位数,得到下图,类1-4可以看做死亡率极低、低、中、高等四类。
点击查看绘图的 R 代码
# 根据给定的高度或者类别数目切割树状图,返回一个向量,表示每个观测值所属的类别 cluster <- cutree(hc, k = 4) # 对数据按照给定的因子进行分组,并应用指定的函数 centers <- aggregate(data.c2[, -1], by = list(cluster), FUN = median) centers <- as.data.table(centers) centers.m <- melt(centers, id = 1) centers.m[, ':='( variable_new = factor( variable, levels = c( '1-4岁', '5-9岁', '10-14岁', '15-19岁', '20-24岁', '25-29岁', '30-34岁', '35-39岁', '40-44岁', '45-49岁', '50-54岁', '55-59岁', '60-64岁', '65-69岁', '70-74岁', '75-79岁' ) ), group_new = factor(Group.1, levels = c(1, 2, 3, 4)) )] |> ggplot(mapping = aes(x = variable_new, y = value, fill = group_new)) + geom_bar(stat = 'identity', position = 'dodge') + facet_grid(cols = vars(group_new)) + labs(x = '', y = '人口死亡率(千分率)', fill = '类别') + theme(axis.text.x = element_blank())
5.4.2. 因子分析 🔗
本小节做因子分析使用的数据依然是在2019.11.1-2020.10.31的1-79岁人群的死亡率数据。因子分析相当于将1-79岁的16个年龄段死亡率指标转换成了两个不完全独立的因子。当然,解读因子分析结果时,极重要的部分是归纳因子所涵盖的含义,本节忽略这一部分,在绘制各样本的因子得分图时隐藏了中心点向指向各年龄段的箭头。
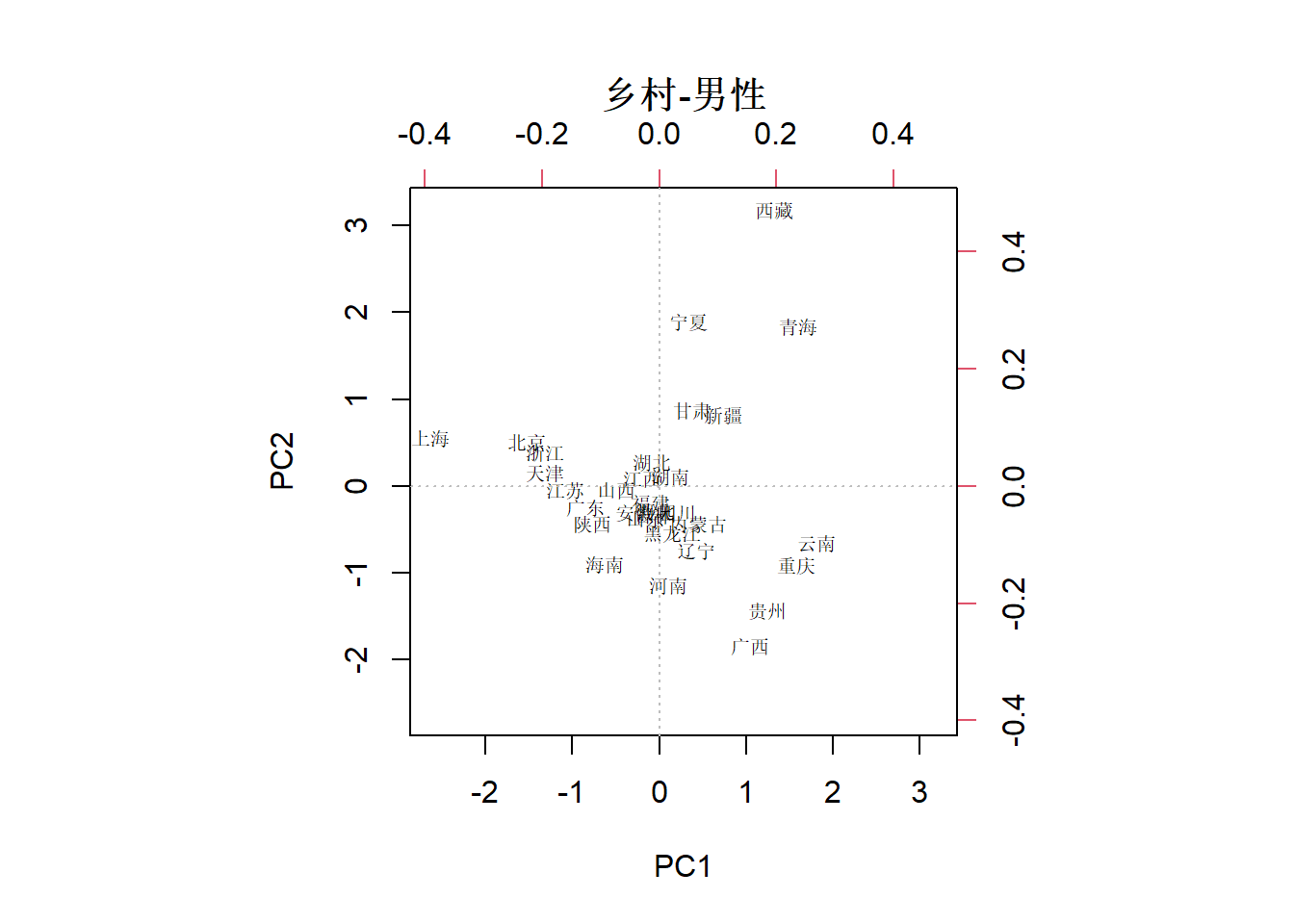
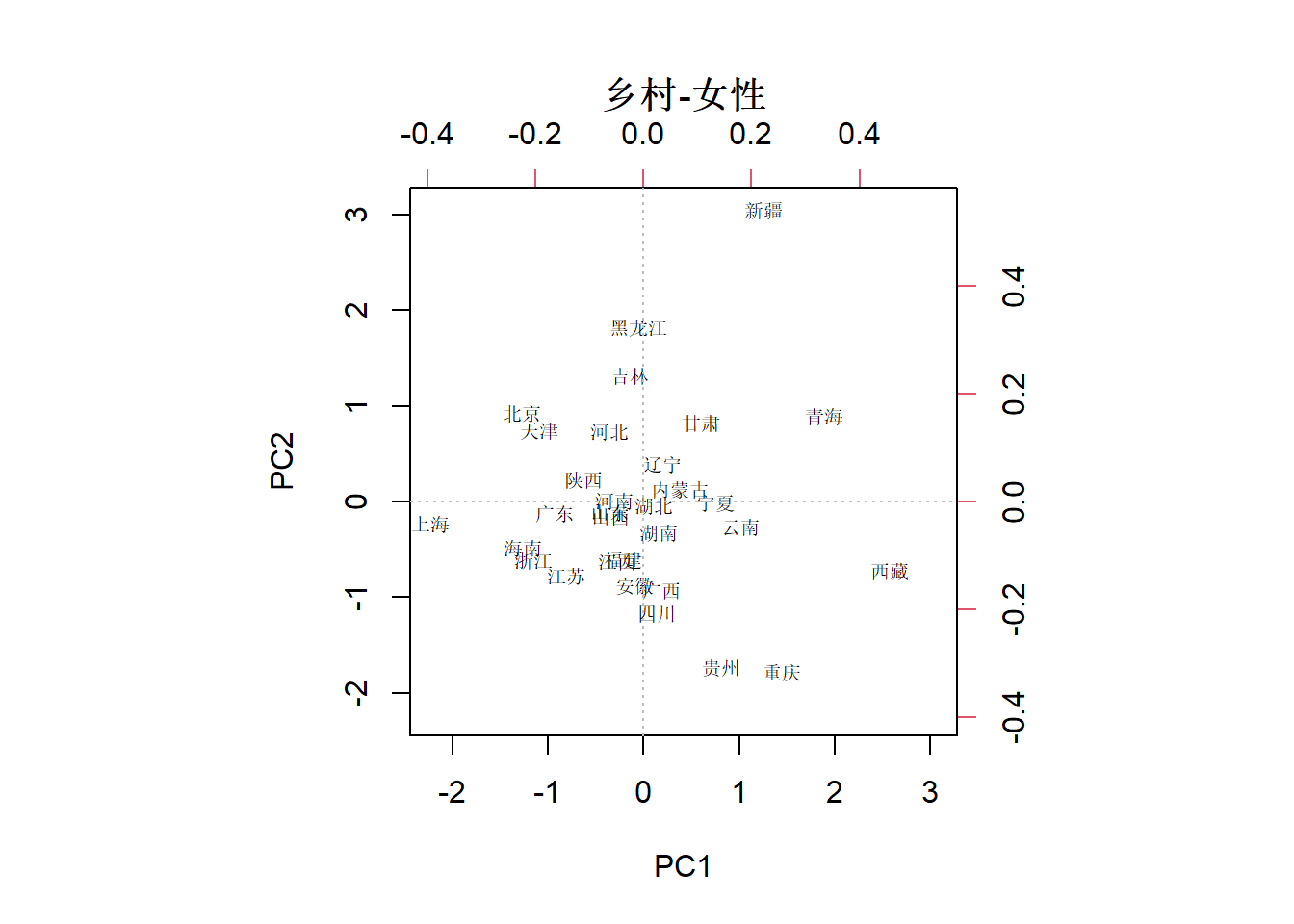
下面的因子得分图所使用的数据范围限定于“乡村-男性”,可粗略看做从左到右各年龄段死亡率逐渐升高,上海在图中最左边亦即死亡率最低。
点击查看因子分析的 R 代码
library(psych) #library(GPArotation) # 计算样本相关矩阵 data.a <- data.c1[, -1] R <- cor(data.a) # kmo检验,KMO值大于0.8表示很适合做因子分子 #KMO(data.a) # Bartlett 检验,p之小于0.01表示适合做因子分子 #bartlett.test(data.a) # 碎石图 # par(mfrow=c(1,1)) # screeplot(princomp(data.a),type="lines") # 用极大似然法做因子分析 # Cumulative Var 表示因子的累积贡献率,前两个累积81% # factanal(data.a, factors = 3, rotation = "none") # 主成分法做因子分析 # Cumulative Var 看累积贡献率,前两个累积达到87% # psych::principal(data.a, nfactors = 3, rotate = "none") # 主成分法,方差最大化做因子正交旋转,效果变差 # psych::principal(data.a, nfactors = 3, rotate = "varimax") fac <- psych::principal(data.a, nfactors = 2, rotate = "none") # 绘制因子载荷图 #plot(fac$loadings, xlab = '因子1', ylab = '因子2') # 绘制每个区域的因子得分图 # 此图中从中心点向所有年龄段的箭头指向都是向右 biplot( x = fac$scores, y = fac$loadings, cex = .7, expand = 2, # 默认expand = 1展示第二组点,即本例中的年龄段,改成2则隐藏 arrow.len = 0, # 设置箭头长度为0,隐藏箭头 var.axes = FALSE, # 隐藏箭身 main = '乡村-男性') abline(h = 0, v = 0, col = "gray", lty = 3)
下面的因子得分图所使用的数据范围限定于“乡村-女性”,初步结论与上图近似。
点击查看因子分析的 R 代码
# 计算样本相关矩阵 data.b <- data.c2[, -1] R <- cor(data.b) #cor.plot(R) # kmo检验,KMO值大于0.8表示很适合做因子分子 #KMO(data.b) # Bartlett 检验,p之小于0.01表示适合做因子分子 #bartlett.test(data.b) # 碎石图 # par(mfrow=c(1,1)) # screeplot(princomp(data.b),type="lines") # 用极大似然法做因子分析 # Cumulative Var 表示因子的累积贡献率,前两个累积86%,因素之间区分不开 # factanal(data.b, factors = 3, rotation = "none") # 主成分法做因子分析 # Cumulative Var 看累积贡献率,前两个累积达到88% # psych::principal(data.b, nfactors = 3, rotate = "none") # 主成分法,方差最大化做因子正交旋转,效果变差 # psych::principal(data.b, nfactors = 3, rotate = "varimax") fac <- psych::principal(data.b, nfactors = 2, rotate = "none") # 绘制因子载荷图 #plot(fac$loadings, xlab = '因子1', ylab = '因子2') # 绘制每个区域的因子得分图 biplot( x = fac$scores, y = fac$loadings, cex = .7, expand = 2, # 默认expand = 1展示第二组点,即本例中的年龄段,改成2则隐藏 arrow.len = 0, # 设置箭头长度为0,隐藏箭头 var.axes = FALSE, # 隐藏箭身 main = '乡村-女性') abline(h = 0, v = 0, col = "gray", lty = 3)
6. 附录 🔗
6.1. 部分 echart4r 代码 🔗
library(echarts4r)
# 死亡人口数
data.age[type == '不分城乡' & year == '2019.11.1-2020.10.31' &
age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)))] |>
group_by(age_new2) |>
e_charts(year) |>
e_bar(dead_all)
# 总人口数
data.age[type == '不分城乡' & year == '2019.11.1-2020.10.31' &
age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)))] |>
group_by(age_new2) |>
e_charts(year) |>
e_bar(population_all)
# 死亡率
data.age[type == '不分城乡' & year == '2019.11.1-2020.10.31' &
age %in% c(0:99), ][, ':='(age_new2 = factor(age, levels = c(0:99)))] |>
group_by(age_new2) |>
e_charts(year) |>
e_bar(dead_rate_all)
6.2. DT 代码 🔗
library(DT)
datatable(
data,
options = list(dom = 'tp'),
filter = list(
position = 'top',
# 可选参数值有"none", "bottom", "top"
clear = TRUE,
# 是否展示在筛选框中输入过滤条件后的清除按钮
plain = FALSE
)
)
6.3. 数据说明 🔗
数据来源有三:
整理数据除了将不同年份、相同维度的数据合并在一起,还有以下几处整合。
- 将2020年数据中“未上过学”和“学前教育”合并汇总为“未上过学”,将“硕士研究生”和“博士研究生”合并为“研究生”。
- 将2000年数据中“未上过学”和“扫盲班”合并为“未上过学”,将“高中”和“中专”合并为“高中”。
- 将2000年数据中“初婚有配偶”和“再婚有配偶”合并为“有配偶”。
| sheet 表序号 | 对应内容 | 对应来源 |
|---|---|---|
| 1 | 各地区分性别、月份的死亡人口 | 2020:1-11 各地区分性别、月份的死亡人口(2019.11.1-2020.10.31) 2020:1-11 各地区分性别、月份的死亡人口(2019.11.1-2020.10.31)(城市) 2020:1-11 各地区分性别、月份的死亡人口(2019.11.1-2020.10.31)(镇) 2020:1-11 各地区分性别、月份的死亡人口(2019.11.1-2020.10.31)(乡村) 2010:1-7 各地区分性别、月份的死亡人口(2009.11.1-2010.10.31) 2000:表1—13 省、自治区、直辖市分性别、月份的死亡人口(1999.11.1-2000.10.31) |
| 2 | 各地区分年龄、性别的死亡人口 | 2020:6-1 各地区分年龄、性别的死亡人口(2019.11.1-2020.10.31) 2020:6-1a 各地区分年龄、性别的死亡人口(2019.11.1-2020.10.31)(城市) 2020:6-1b 各地区分年龄、性别的死亡人口(2019.11.1-2020.10.31)(镇) 2020:6-1c 各地区分年龄、性别的死亡人口(2019.11.1-2020.10.31)(乡村) 2010:6-1 各地区分年龄、性别的死亡人口(2009.11.1-2010.10.31) 2010:6-1a 各地区分年龄、性别的死亡人口(2009.11.1-2010.10.31)(城市) 2010:6-1b 各地区分年龄、性别的死亡人口(2009.11.1-2010.10.31)(镇) 2010:6-1c 各地区分年龄、性别的死亡人口(2009.11.1-2010.10.31)(乡村) 2000:表6—1 省、自治区、直辖市分性别、年龄的死亡人口(1999.11.1-2000.10.31) 2000:表6—1a 省、自治区、直辖市分性别、年龄的死亡人口(城市)(1999.11.1-2000.10.31) |
| 3 | 各地区分性别、受教育程度的3岁及以上死亡人口 | 2020:6-2 各地区分性别、受教育程度的3岁及以上死亡人口(2019.11.1-2020.10.31) 2020:6-2a 各地区分性别、受教育程度的3岁及以上死亡人口(2019.11.1-2020.10.31)(城市) 2020:6-2b 各地区分性别、受教育程度的3岁及以上死亡人口(2019.11.1-2020.10.31)(镇) 2020:6-2c 各地区分性别、受教育程度的3岁及以上死亡人口(2019.11.1-2020.10.31)(乡村) 2010:6-2 各地区分性别、受教育程度的6岁及以上死亡人口(2009.11.1-2010.10.31) 2010:6-2a 各地区分性别、受教育程度的6岁及以上死亡人口(2009.11.1-2010.10.31)(城市) 2010:6-2b 各地区分性别、受教育程度的6岁及以上死亡人口(2009.11.1-2010.10.31)(镇) 2010:6-2c 各地区分性别、受教育程度的6岁及以上死亡人口(2009.11.1-2010.10.31)(乡村) 2000:表6—2 省、自治区、直辖市分性别、受教育程度的6岁及6岁以上死亡人口(1999.11.1-2000.10.31) |
| 4 | 各地区分性别、婚姻状况的15岁及以上死亡人口 | 2020:6-3 各地区分性别、婚姻状况的15岁及以上死亡人口(2019.11.1-2020.10.31) 2020:6-3a 各地区分性别、婚姻状况的15岁及以上死亡人口(2019.11.1-2020.10.31)(城市) 2020:6-3b 各地区分性别、婚姻状况的15岁及以上死亡人口(2019.11.1-2020.10.31)(镇) 2020:6-3c 各地区分性别、婚姻状况的15岁及以上死亡人口(2019.11.1-2020.10.31)(乡村) 2010:6-3 各地区分性别、婚姻状况的15岁及以上死亡人口(2009.11.1-2010.10.31) 2010:6-3a 各地区分性别、婚姻状况的15岁及以上死亡人口(2009.11.1-2010.10.31)(城市) 2010:6-3b 各地区分性别、婚姻状况的15岁及以上死亡人口(2009.11.1-2010.10.31)(镇) 2010:6-3c 各地区分性别、婚姻状况的15岁及以上死亡人口(2009.11.1-2010.10.31)(乡村) 2000:表6—3 省、自治区、直辖市分性别、婚姻状况的15岁及15岁以上死亡人口(1999.11.1-2000.10.31) |
| 5 | 全国分年龄、性别的死亡人口状况 | 2020:6-4 全国分年龄、性别的死亡人口状况(2019.11.1-2020.10.31) 2020:6-4a 全国分年龄、性别的死亡人口状况(2019.11.1-2020.10.31)(城市) 2020:6-4b 全国分年龄、性别的死亡人口状况(2019.11.1-2020.10.31)(镇) 2020:6-4c 全国分年龄、性别的死亡人口状况(2019.11.1-2020.10.31)(乡村) 2010:6-4 全国分年龄、性别的死亡人口状况(2009.11.1-2010.10.31) 2010:6-4a 全国分年龄、性别的死亡人口状况(2009.11.1-2010.10.31)(城市) 2010:6-4b 全国分年龄、性别的死亡人口状况(2009.11.1-2010.10.31)(镇) 2010:6-4c 全国分年龄、性别的死亡人口状况(2009.11.1-2010.10.31)(乡村) 2000:表6—4 全国分年龄、性别的死亡人口状况(1999.11.1-2000.10.31) 2000:表6—4a 全国分年龄、性别的死亡人口状况(1999.11.1-2000.10.31)(城市) 2000:表6—4b 全国分年龄、性别的死亡人口状况(1999.11.1-2000.10.31)(镇) 2000:表6—4c 全国分年龄、性别的死亡人口状况(1999.11.1-2000.10.31)(乡村) |
| 6 | 各地区分年龄、性别的人口 | 2020:1-5 各地区分年龄、性别的人口 2020:1-5a 各地区分年龄、性别的人口(城市) 2020:1-5b 各地区分年龄、性别的人口(镇) 2020:1-5c 各地区分年龄、性别的人口(乡村) 2010:1-7 各地区分年龄、性别的人口 2010:1-7a 各地区分年龄、性别的人口(城市) 2010:1-7b 各地区分年龄、性别的人口(镇) 2010:1-7c 各地区分年龄、性别的人口(乡村) 2000:表1—7 省、自治区、直辖市分性别、年龄的人口 2000:表1—7a 省、自治区、直辖市分性别、年龄的人口(城市) 2000:表1—7b 省、自治区、直辖市分性别、年龄的人口(镇) 2000:表1—7c 省、自治区、直辖市分性别、年龄的人口(乡村) |
| 7 | 各地区分性别、受教育程度的3岁及以上人口 | 2020:1-6 各地区分性别、受教育程度的3岁及以上人口 2020:1-6a 各地区分性别、受教育程度的3岁及以上人口(城市) 2020:1-6b 各地区分性别、受教育程度的3岁及以上人口(镇) 2020:1-6c 各地区分性别、受教育程度的3岁及以上人口(乡村) 2010:1-8 各地区分性别、受教育程度的6岁及以上人口 2010:1-8a 各地区分性别、受教育程度的6岁及以上人口(城市) 2010:1-8b 各地区分性别、受教育程度的6岁及以上人口(镇) 2010:1-8c 各地区分性别、受教育程度的6岁及以上人口(乡村) 2000:表1—8 省、自治区、直辖市分性别、受教育程度的6岁及6岁以上人口 |
| 8 | 各地区分性别、婚姻状况的15岁及以上人口 | 2020:5-1 各地区分性别、婚姻状况的15岁及以上人口 2020:5-1a 各地区分性别、婚姻状况的15岁及以上人口(城市) 2020:5-1b 各地区分性别、婚姻状况的15岁及以上人口(镇) 2020:5-1c 各地区分性别、婚姻状况的15岁及以上人口(乡村) 2010:5-1 各地区分性别、婚姻状况的15岁及以上人口 2010:5-1a 各地区分性别、婚姻状况的15岁及以上人口(城市) 2010:5-1b 各地区分性别、婚姻状况的15岁及以上人口(镇) 2010:5-1c 各地区分性别、婚姻状况的15岁及以上人口(乡村) 2000:表5—1 省、自治区、直辖市分性别、婚姻状况的15岁及15岁以上人口 2000:表5—1:a 省、自治区、直辖市分性别、婚姻状况的15岁及15岁以上人口(城市) 2000:表5—1b 省、自治区、直辖市分性别、婚姻状况的15岁及15岁以上人口(镇) 2000:表5—1c 省、自治区、直辖市分性别、婚姻状况的15岁及15岁以上人口(乡村) |
-
翻看了几篇以死亡率为主题的文章,如中国高龄老人健康状况和死亡率的变动趋势分析、中国人口死亡率随机预测模型的比较与选择、中国死亡率改善率预测及实践研究,偏重于用一些模型作为工具去分析。也特地翻了一些解读七普数据的文章,如七普公报详细解读——特别回应数据之惑,死亡人口数据看上去没什么疑惑或争议,顺便再翻了翻人大人口与发展研究中心的其他文章如《世界人口展望(2019)》预测方案与参数设置、关注“新一代”老年人口的新特点等,对死亡的谈论总是只占很小的篇幅。 ↩︎
-
尽管日出和日落都很好看,但在人类社会里生存与发展才是第一要素,几千年累积的时间观念和文化氛围里也始终将日出曙光关联上初升的希望,将日落余晖关联上宁静的消逝,黑夜里满天的星辰只会寄宿着人们对逝去的怀念。 ↩︎
-
在图例项较多的情况下,用 ggplot2 绘制的图形很难看出哪一项图例对应哪个柱子,这里我是用 echarts4r 绘图来查看的。 ↩︎
-
第215页开始的第八节妇幼保健与计划生育,有围产儿死亡率、孕产妇建卡率、孕产妇死亡率等指标的具体含义。活产数,指年内妊娠满28周及以上(如孕周不清楚,可参考出生体重达1000克及以上),娩出后有心跳、呼吸、脐带搏动、随意肌收缩4项生命体征之一的新生儿数。围产儿死亡率,指孕满28周或出生体重≥1000克的胎儿(含死胎、死产)至产后7天内新生儿死亡数与活产数(孕产妇)之比,一般以‰表示。孕产妇建卡率,指年内孕产妇中由保健人员建立的保健卡(册)人数与活产数之比,一般用%表示。孕产妇死亡率 指年内每10万名孕产妇的死亡人数。孕产妇死亡指从妊娠期至产后42天内,由于任何妊娠或妊娠处理有关原因导致的死亡,但不包括意外原因死亡者。按国际通用计算方法,“孕产妇总数”以“活产数”代替计算。 ↩︎
-
在第218页展示的表8-3 儿童保健情况,2019年全国的围产儿死亡率是4.02,而西藏的围产儿死亡率最高达到了12.64。在第220页展示的表8-4-2 2019年各地区孕产妇保健情况,全国的孕产妇建卡率为92.4%,而西藏只有66.8%。在第221页的8-4-2续表,2019年全国的孕产妇死亡率(1/10万)市级为8.9、县级为11.8,而西藏市级为17.7、县级为68.8。 ↩︎
-
以前当然有用过聚类,一些基本的分类、回归、聚类方法的名字和基本原理都跟刻在脑子里一样印象很深,但其实只记得大概,很多细节还是自然遗忘了。有心从零开始重新积累,先翻了翻 CRAN 的任务视图,戳进去聚类(Cluster)页面瞅了瞅,这页就是按聚类方法先分大类,然后再分别描述每个包可以做什么,缺少一些方法之间的优缺点对比,于是理所当然又去翻了翻Python 的 scikit-learn 的网页,瞅了瞅聚类的部分,此文档还有中文版。感觉讲得最好的还是《多元统计分析》的课本,先从各种距离的度量和相似度开始讲起,如明式距离、欧式距离、马式距离、余弦相似度等,然后从八种系统聚类方法引出类与类之间距离的定义如最大距离法、最小距离法等,最后从系统聚类法(层次聚类)延伸出如 K 均值聚类、K 近邻等更多聚类方法。后来工作了又接触了高斯混合聚类,从更多的机器学习书籍中了解到除了基于距离的聚类,还有基于密度的聚类、基于网格的聚类、基于模型的聚类等。然鹅,吐槽这么多,只是让我意识到了记笔记的重要性…… ↩︎